Grundlegende Algorithmen in der Bildverarbeitung

Korbinian

Für PDF Fans: www.korbinian-riedhammer.de/misc/BVAlgos.pdf

Grundlegende Algorithmen in der Bildverarbeitung

Inhalt:

Einleitung
Rotation von Bildern
2.1 Octave Implementierung
2.2 c++ Implementierung
Preprocessing von Bildern
3.1 Einfache Filter
3.2 Implementierung einfacher Filter in Octave
3.3 Implementierung einfacher Filter in c++
3.4 Effektive Implementierung eines 3x3 Gaussfilters
Erweiterte Filter
4.1 Thresholding
4.2 Medianfilter
4.3 Histogram Equilisation
Defektpixelinterpolation
5.1 Octave Implementierung

1 Einleitung

In diesem Artikel möchte ich einige grundlegende Verfahren vorstellen, die in der Bildverarbeitung regen Einsatz finden. Ich werde jedes Verfahren zunächst beschreiben, dann anhand eines Octave Skriptes veranschaulichen, und schließlich (fragmentweise) in c++ implementieren. Diese Implementierungen sind i.d.R. nicht die schnellsten, da ich auf Anschaulichkeit Wert gelegt habe.
Warum benutze ich Octave, um die Algorithmen zu veranschaulichen, obwohl der Leser vermutlich nur an der c++ Variante interessiert ist? Zum einen, weil Octave Programmtext deutlich übersichtlicher und damit leichter nachzuvollziehen ist. Meines Erachtens wichtiger ist aber, daß es gerade in der Bildverarbeitung praktisch ist, mit diesem Tool vertraut zu sein, da man oft ein Verfahren erst einmal ausprobieren möchte, bevor man es implementiert. Würde man sofort anfangen, die Idee in c++ zu implementieren, so hat man erst einmal einen größeren Zeitaufwand, dann das größere Risiko, einen Fehler darin zu haben, und letztendlich verfängt man sich leicht in Startschwierigkeiten wie "`wie lese ich ein Bild ein"'. Alles das wird durch die abstraktere Implementierung in Octave verhindert.
Neben den trivialen Implementierungen werde ich auch eine Effektive am Beispiel eines Filters zeigen, die nicht nur wegen den Programmiertricks so gut ist, sondern weil mathematische Umstände zu unserem Vorteil genutzt werden. Ich zeige das, um den Leser auch für die Theorie hinter den Verfahren zu interessieren. Oft entstehen neue schnelle Lösungen, weil die Probleme von einer anderen Seite betrachtet werden.

2 Rotation von Bildern

Oftmals sind die Bilder nicht in der Position, in der man sie gerne hätte. Das liegt zum einen daran, dass die Kamera oder der Detektor nicht korrekt angebracht sind, oder ganz einfach das Objekt nicht in der richtigen Lage ist, wie z.B. schiefe Fotos oder schiefe Zeilen in der Schrifterkennung. Rotationen im zweidimensionalen Raum lassen sich mathematisch recht einfach darstellen: Sei p ein zu rotierender und q der rotierte Punkt, so besteht folgender Zusammenhang mit der Rotationsmatrix R resultierend aus dem Rotationswinkel omega:
$R = \left( \begin{array}{cc} \cos\omega & -\sin\omega \\ \sin\omega & \cos\omega \end{array} \right)$
$q = Rp$
Möchte man nun eine Rotation eines ganzen Bildes durchführen, so berechnet man für jeden Punkt aus dem Urbild die Koordinaten im rotierten Bild. Bei der Implementierung ist auf ungültige Koordinaten zu achten: Das kann zum einen ein Nichtbeachten von nicht erreichbaren Koordinaten sein, zum anderen eine Expansion des Bildes (bei Winkeln ungleich 90, 180 und 270 Grad). Der Einfachheit halber werde ich hier Ersteres zeigen. Punkte im Bild, denen kein Punkt aus dem Urbild zugewiesen wird, bleiben z.B. schwarz. Nimmt man nun die "Vorwärtsabbildung" so kann es sein, dass manche Pixel aufgrund von Rundungsfehlern nicht rotiert werden. Dem kann man entgegenkommen, indem man nicht von Urbild nach Bild rechnet sondern umgekehrt, und optional beim Zugriff interpoliert (z.B. bilinear). Damit wird jedem Pixel im Bild ein (interpoliertes) Pixel aus dem Urbild zugeordnet, was umgekehrt aufgrund der Diskretisierung nicht der Fall ist.

2.1 Octave Implementierung

% Rotieren eines weissen Vierecks um 30 Grad um
% den Ursprung

dim = 30;
w = -(pi/6);

% Bild und Urbild reservieren
Bild   = zeros(dim);
Urbild = zeros(dim);

% Weissen Rand und Viereck zeichnen
Urbild(10:20, 10:20) = 255;
Urbild(:,2)  = 255;
Urbild(:,29) = 255;
Urbild(2,:)  = 255;
Urbild(29,:) = 255;

for i=1:dim
  for j=1:dim
    x = round(i*cos(w)-j*sin(w));
    y = round(i*sin(w)+j*cos(w));
    if (x > 0 && x <= dim && y > 0 && y <= dim)
      Bild(i,j) = Urbild(x,y);
    endif
  endfor
endfor

Beispielbilder

Urbild
Bild, 30 Grad rotiert

2.2 c++ Implementierung

template <typename T>
void rotate(T* din, T* dout, unsigned sx, unsigned sy, double w)
{
    for (unsigned i = 0; i < sy; ++i)
    {
        for (unsigned j = 0; j < sx; ++j)
        {
            signed rx = (signed)((double)j*cos(w) - (double)i*sin(w));
            signed ry = (signed)((double)j*sin(w) + (double)i*cos(w));
            if (rx < 0 || ry < 0 || rx >= sx || ry >= sy)
                continue;
            dout[i*sx + j] = din[ry*sx + rx];
        }
    }
    return;
}

3 Preprocessing von Bildern

Normalerweise werden Bilder vor ihrer Verarbeitung erst vorbereitet, um bessere Eingangsbedingungen für die eigentlichen Algorithmen zu haben. Unter einem Filter verstehe ich eine Operation, die ein Bild verändert. Ich möchte hier zuerst einfache Filter vorstellen, die auf einer Faltung zweier Bilder beruhen, und dann erweiterte Filter, die teils aus mathematischen Ideen resultieren, und nichts mit Faltung zu tun haben.

3.1 Einfache Filter

Bei einfachen Filtern wird das Urbild mit einem Filterkernel gefaltet. Mathematisch ist die Faltung zweier Bilder im Diskreten für die Bildfunktionen f und g so beschrieben:
$(f * g)(n) = \sum_k{f(k)g(n-k)}$
Da allerdings der Filterkernel normalerweise eine Dimension von 3x3 oder 5x5 hat, keinenfalls aber die Größe des Urbilds, wird das Urbild abschnittweise mit dem Kernel gefaltet. Praktisch gesehen ist das eine Multiplikation der jeweils überlappenden Matrixelemente (was sich im c++ Code gut sehen lässt). Kernelgrößen sind im Allgemeinen ungerade, damit beim Programmieren immer die Mitte des Kernelfensters eindeutig ist.
Bei der hier gezeigten c++ Implementierung wird der Rand (also die Pixel, für die die Filtermaske nicht vollständig gefüllt ist) nicht gefiltert. Ein besseres Verfahren ist z.B. die fehlenden Werte mit 0 anzunehmen. Die Implementierung ist desweiteren nicht gerade die Effektivste: Für jedes Pixel wird das Kernelfenster neu aufgestellt. Ist die Kernelgröße im vornherein bekannt, so kann man effektivere Implementierungen schreiben, indem man sich Pointerarithmetik zu Hilfe nimmt. Als Beispiel eines effektiv implementierten Filters zeige ich eine elegante Version des 3x3 Gauß Filter, der sich neben der Pointerarithmetik noch folgende Eigenschaft zunutze macht: Die zweifache Anwendung des 2x2 Mittelwertfilters entspricht der einfachen Anwendung eines 3x3 Gaussfilters.

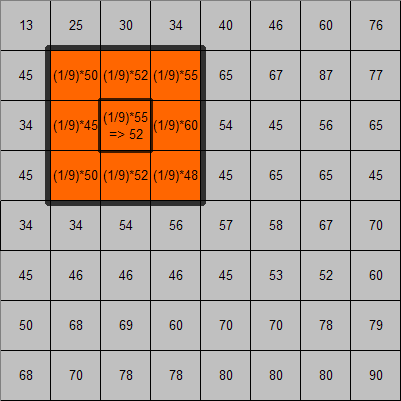
Verknüpfung von Kernel- und Bildelementen beim 3x3 Mittelwertfilter

Beispiele für einfache Filter

Mittelwert: Der Mittelwertfilter wird in verschiedenen Kernelgrößen verwendet und bildet jeweils den Mittelwert über die Umgebung. Kernelgrößen zwischen 2 und 5 sind gebräuchlich.
$M = \frac{1}{4}\left( \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$
Gaußfilter: Der Gaussfilter wird in Kernelgrößen ab 3 verwendet, die Elemente sind entsprechend der Gaußverteilung erstellt. Er erzielt eine bessere Glättung des Bildes als ein Mittelwertfilter, da die Pixel von außen nach innen immer mehr an Einfluss erhalten.
$G = \frac{1}{16} \left( \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array} \right)$
Kantenerkennung, finite Differenz: Der einfache Kantenerkennungsfilter beruht auf der Idee der finiten Differenzen. Betrachtet man das Bild als zweidimensionale diskrete Funktion, so kann man mit Hilfe des Differenzenquotienten die Steigung für x und y Richtung an jedem Punkt berechnen. Auf diese Weise erhält man kleine Werte, wenn sich der Farb-/Grauwert kaum ändert, und große Werte, wenn von einem Pixel zum nächsten ein starker An-/Abstieg ist. Die beiden gezeigten Kernel sind die sog. forward difference Kernel für x und y Richtung.
$B\_x = \left( \begin{array}{cc} -1 & 1 \end{array} \right); B\_y = \left( \begin{array}{c} -1 \\ 1 \end{array} \right)$
Vereinfacht gesagt beruht die Kantenerkennung durch finite Differenzen auf den Unterschieden von einem zum nächsten Pixel in jede Bildrichtung: Ändert sich der Farbwert stark, so ist die Differenz groß und eine Kante liegt vor. Ändert er sich aber kaum, so wird ein homogenes Gebiet vorliegen.
Sobelfilter: Der Sobelfilter funktioniert ähnlich wie der einfache Kantenerkennungsfilter, nur dass er die Nachbarschaft mit in Betracht zieht:
$S\_x = \left( \begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array} \right); S\_y = \left( \begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array} \right)$

3.2 Implentierung einfacher Filter in Octave

% Einfache Filter

% Weisses Viereck auf schwarzem Untergrund
img = zeros(30);
img(10:20, 10:20) = 1;

M  = (1/4)*[1 1; 1 1];
G  = (1/16)*[1 2 1; 2 4 2; 1 2 1 ];
Dx = [-1 1];
S  = (1/8)*[-1 0 1; -2 0 2; -1 0 1 ];

img_m = conv2(img, M, 'same');
img_g = conv2(img, G, 'same');
img_x = conv2(img, Dx, 'same');
img_s = conv2(img, S, 'same');

Originalbild Mittelwertfilter Gaußfilter Kanten in X Richtung Sobel in X Richtung

3.3 Implementierung einfacher Filter in c++

void filter(double *din, double *dout, unsigned sx, unsigned sy, double *kernel, unsigned kdim)
{
    for (unsigned y = (kdim/2); y < sy - (kdim/2); ++y)
        for (unsigned x = (kdim/2); x < sx - (kdim/2); ++x)
        {
            dout[y*sx+x] = 0.;
            for (unsigned i = 0; i < kdim; ++i)
                for (unsigned j = 0; j < kdim; ++j)
                    dout[y*sx+x] += (kernel[i*kdim+j] * din[(y+j-kdim/2)*sx + x+i-kdim/2];
        }
}

3.4 Effektive Implementierung eines 3x3 Gaussfilters

Wie eingangs erwähnt beruht diese Implementierung auf der Äquivalenz der zweifachen 2x2 Mittelwertfilterung zur 3x3 Gaussfilterung (wer's nicht glaubt nehme ein Blatt Papier, und rechne es nach :-). Daraus ergeben sich zwei Vorteile: Zum einen ist das Fenster auf 2x2 geschrumpft, zum anderen sind die Gewichte für die Felder jetzt immer 0.25 statt vorher zwischen 0.0625 und 0.25, was die Berechnung erleichtert: man kann im voraus alle Werte mal 0.25 nehmen, so muss man beim Durchlaufen nur noch zusammenzählen. Es werden somit 4 Pointer für das Kernelfenster und einer für das Outputfeld benutzt. Jetzt ist nur Vorsicht geboten: Wendet man den gleichen Filter zwei mal an, so stimmt das Ergebnis nicht. Das Outputfenster muss einmal an (0,0) und einmal an (1,1) liegen.
Nimmt man alles das zusammen, so erhält man folgende Implementierung:

void gaussian3filter(double *img, double *buf, unsigned sx, unsigned sy)
{
    // this is a 3x3 gaussian filter realized by 2 2x2 mean value filters
    double *pass1 = buf;
    double *pass2 = img+sx+1;
    // first pass ptrs
    double *p1_1 = img;
    double *p1_2 = img+1;
    double *p1_3 = img+sx;
    double *p1_4 = img+sx+1;
    // second pass ptrs
    double *p2_1 = buf;
    double *p2_2 = buf+1;
    double *p2_3 = buf+sx;
    double *p2_4 = buf+sx+1;
    // perform 2 line of 1st pass
    for (unsigned i = 0; i < sx-1; ++i)
        *pass1++ = .25*((*p1_1++) + (*p1_2++) + (*p1_3++) + (*p1_4++));
    // skip last field
    ++pass1; ++p1_1; ++p1_2; ++p1_3; ++p1_4;
    // 1 line more to go
    for (unsigned i = 0; i < sx-1; ++i)
        *pass1++ = .25*((*p1_1++) + (*p1_2++) + (*p1_3++) + (*p1_4++));
    ++pass1; ++p1_1; ++p1_2; ++p1_3; ++p1_4;
    // now continue with the 1st pass, but work on 2nd in parralel
    for (unsigned i = 2; i < sy-1; ++i) // we start in line 3
    {
        for (unsigned j = 0; j < sx-1; ++j)
        {
            *pass1++ = .25*((*p1_1++) + (*p1_2++) + (*p1_3++) + (*p1_4++));
            *pass2++ = .25*((*p2_1++) + (*p2_2++) + (*p2_3++) + (*p2_4++));
        }
        ++pass1; ++p1_1; ++p1_2; ++p1_3; ++p1_4;
        ++pass2; ++p2_1; ++p2_2; ++p2_3; ++p2_4;
    }
    // 2 more lines for 2nd pass
    for (unsigned i = 0; i < sx-1; ++i)
        *pass2++ = .25*((*p2_1++) + (*p2_2++) + (*p2_3++) + (*p2_4++));
    // skip last field
    ++pass2; ++p2_1; ++p2_2; ++p2_3; ++p2_4;
    // 1 line more to go
    for (unsigned i = 0; i < sx-1; ++i)
        *pass2++ = .25*((*p2_1++) + (*p2_2++) + (*p2_3++) + (*p2_4++));
}

4 Erweiterte Filter

Natürlich gibt es noch andere Filter, die nicht auf der Faltung von Urbild mit Kernel basieren. Sie machen sich meist andere Eigenschaften von realen Bildern oder unseres Perzeptionsmechanismus zunutze. Da die Implementierungen recht einfach sind und kaum Hilfsfunktionen benötigen, verzichte ich hier auf die Octave Variante.

4.1 Thresholding

Beim Thresholding wird, wie der Name schon sagt, ein Schwellwert festgelegt, und dementsprechend pixelweise für einen bestimmten Wert entschieden. Meistens benutzt man es, um s/w Bilder zu erhalten, man kann das Verfahren allerdings auch auf mehrere Farben auslegen, z.B. bei der Farbraumumwandlung von 16bit auf 8bit bei Farb- oder Grauwertbildern. Da dieser Filter so trivial ist, werde ich keine Implementierung zeigen.

4.2 Medianfilter

Dem Namen nach ähnelt er dem Mittelwertfilter aus dem vorigen Kapitel. Das dahinter liegende Verfahren ist jedoch ein komplett anderes: Die Farb-/Grauwerte werden über eine gewisse Fenstergröße (Kernelsize) in ein Array kopiert und sortiert, und dann das Pixel auf den Wert gesetzt, der in der Mitte dieses Arrays steht. Sinn dieses Verfahrens ist z.B. in Kombination mit dem Differenzbildverfahren Inhomogenitäten festzustellen: Weicht ein Pixel zu stark von seiner Umgebung ab, so liegt vermutlich eine Unregelmäßigkeit vor (bei Gusseisenteilprüfung z.B. ein Gasbläschen).
Der Vorteil des Medianfilters gegenüber dem Mittelwertfilter ist, dass diese Methode sehr ausreißerstabil ist. Wenn sich unter der Filtermaske viele Pixel gleicher Helligkeit befinden und einzelne sehr verschiedene, so haben diese keinen Einfluss auf den resultierenden Helligkeitswert. Die empfohlene Filtergröße liegt bei 7-13, je nach Verwendung.

template<type T>
void medianFilter(T *din, T *dout, unsigned sx, unsigned sy, unsigned ks)
{
    T *values = new T[ks*ks];
    for (unsigned y = (ks/2); y < sy - (ks/2); ++y)
    {
        for (unsigned x = (ks/2); x < sx - (ks/2); ++x)
        {
            // Werte aufsammeln
            for (unsigned i = 0; i < ks; ++i)
                for (unsigned j = 0; j < ks; ++j)
                    values[i*ks + j] = din[(y+j-ks/2)*sx + (x+i-ks/2)];
            // Array sortieren
            std::sort(values, values+(ks*ks));
            // Aktuelles Pixel auf Median setzen
            dout[y*sx + x] = (T)(*(values+(ks/2)));
        }
    }
    delete [] values;
    return;
}

4.3 Histogram Equilisation

Ziel der Histogrammnormalisierung ist eine Verbesserung des Kontrastes und die Glättung des Histogramms. Letztere dient dazu eigentlich gleiche, aber unter verschiedenen Lichtverhältnissen aufgenommene Bilder besser vergleichen zu können. Es wird zuerst ein Histogramm des Bildes erstellt und anschließend normalisiert, sodaß das gesamte Spektrum des Farbraumes (Grauraumes) ausgenutzt wird. Wichtig ist jedoch, daß das Bildformat über einen Helligkeitskanal (YCrCb, HLS, ...) verfügt. Die hier vorgestellte Implementierung arbeitet mit [0;255] Grauwertbildern.
Der Algorithmus:

Erstelle eine Tabelle mit Zuordnung Grauwert-Häufigkeit
Erstelle die laufende Summe
Normalisiere jedes Element der Summe durch Teilung durch die Gesamtsumme
Multipliziere diese Werte mit dem hoechsten Grauwert
Ersetze die neue Grauwerttbelle mit der alten
Aktualisiere das Bild

void histogramEquilisation(unsigned char *din, unsigned char *dout, unsigned sx, unsigned sy)
{
    int container[256];
    std::memset(container, 0, sx*sy);

    // Container fuellen
    for (unsigned y = 0; y < sy; ++y)
    for (unsigned x = 0; x < sx; ++x)
        container[din[y*sx+x]]++;

    // Graymap erstellen
    std::map<unsigned char, int> graymap;
    for (unsigned it = 0; it < 256; ++it)
        if (container[it] < 0)
            graymap[it] = container[it];

    // Laufende Summe bilden
    unsigned char hgval = 0;
    double *sum = new double [graymap.size()]
    std::map<unsigned char, int>::iterator iter = graymap.begin();
    sum[0] = (double)iter->second;
    for (unsigned it = 1, iter++; iter != graymap.end(); ++iter, ++it)
    {
        sum[it] = sum[it-1] + (double)iter->second;
        if (iter->first > hgval)
            hgval = iter->first;
    }

    for (unsigned it = 0; i < graymap.size(); ++it)
        sum[it] = (int)(sum[it] / sum[graymap.size()-1]) * (double)hgval);

    // Bild aktualisieren, dazu Grauwerttabelle anpassen
    for (unsigned it = 0; iter = graymap.begin(); iter != graymap.end(); ++iter, ++it)
        container[iter->first] = (int)sum[it];

    // container enthaelt jetzt die Zuordnung der neuen Grauwerte
    for (unsigned y = 0; y < sy; ++y)
        for (unsigned x = 0; x < sx; ++x)
            dout[y*sx+x] = container[din[y*sx+x]];
}

Originalbild
Bild nach histogram equalisaton

5 Defektpixelinterpolation

Röntgendetektoren, CCD Kameras oder Fingerprintleser haben oft defekte Pixel. An dieser Stelle liefern sie im Normalfall den Mini- oder Maximalwert des Wertebereichs zurück. Bei Röntgendetektoren oder CCD Kameras kann man diese defekten Pixel leicht identifizieren, indem man z.B. ein sog. Hellbild erstellt. Bei Röntgen ist das Vollbelichtung ohne durchstrahltes Objekt, bei CCD starke Überbelichtung ("Hellbild"). Das Ergebnis ist ein weißes Bild, das an den defekten Pixeln schwarz ist. Wiederholt man das mit einem Dunkelbild, so erhält man die entsprechend "anders" defekten Pixel. Hat man die defekten Pixel erst einmal identifiziert, kann man versuchen sie gezielt zu interpolieren. Oftmals genügt ein Mittelwertfilter im betroffenen Gebiet, möchte man allerdings mehr Information wiederherstellen oder ist das defekte Gebiet größer, so bietet sich das sog. band limitaion Verfahren an.
Wem die Fouriertransformation nicht geläufig ist, dem empfehle ich sich zuerst eine gute Erklärung dazu z.B. auf www.wikipedia.org zu lesen
Die Idee: Das Bild wird als zweidimensionales Signal betrachtet. Man nimmt nun an, dass es in realen Bildern keine harten Sprünge in den Farb-/Grauwerten gibt, sondern immer mehr oder weniger weiche Übergänge. Wendet man nun die Fouriertransformation auf ein gewähltes Fenster des Bildes an, so bekommt man das Frequenzspektrum dieses Fensters, welches einem angibt, welche Sinus- oder Cosinusschwingungen man mit welcher Gewichtung überlagern müsste, um das Ausgangssignal zu erhalten. Harte Sprünge würden sich in hohen Frequenzen darstellen, da diese schnell oszillieren und man nur dadurch den geforderten schnellen Farbübergang erreichen kann. Beim band limitation Verfahren werden nun einfach alle Frequenzen oberhalb eines Grenzwertes auf 0 gesetzt, also entfernd. Rekonstruiert man nun das Bildfenster aus diesem modifizierten Frequenzspektrum, so erhält man eine Version des Bildes ohne die schnellen Frequenzen. Abschließend überträgt man die als defekt markierten Pixel von dem rekonstruierten Bild ins Originalbild. Wendet man dieses Verfahren nun iterativ an, so lässt sich die Qualität der Interpolation immer weiter verbessern. Will man das Verfahren noch optimieren, so kann man den Grenzwert bei dem die Frequenzen "abgeschnitten" werden sollen bei jeder Iteration neu bestimmen.
Zu diesem Verfahren biete ich jetzt nur eine Octave Implementierung, da für die c++ Variante eine FFT Bibliothek benötigt würde und dann der Code fast analog zur Octavevariante wäre.
An den Bildern sieht man, dass die Frequenzmethode für größere Fehler nur bedingt nützlich ist. Man könnte das Ergebnis verbessern, indem man eine kleinere Fenstergröße nimmt. Im Beispiel wurde das ganze Bild genommen, was hier einer Fenstergröße von 128 entspricht. Fenstergrößen von 64 Pixel haben sich bewährt.

5.1 Octave Implementierung

% Bild einlesen
org = imread("res/brain_org.png");
[sx, sy] = size(org);
% Welche Frequenzen sollen abgeschnitten werden?
m = 35;
% Ein paar kuenstliche Fehler...
def = org;
def(30, 1:sy) = 256; def(1:sx, 40) = 256;
def(60:65, 60:65) = 256; def(90:95, 60:85) = 256;

% Iterationsschleife
for k = 1 : 10
  defFT = fftshift(fft2(def));
  defFT(1:sx, 1:m) = 0; % Frequenzen abschneiden
  defFT(1:sx, sy-m:sy) = 0;
  defFT(1:m, 1:sy) = 0;
  defFT(sx-m:sx, 1:sy) = 0;  
  recon = ifft2(fftshift(defFT)); % inverse FFT
  def(30, 1:sy) = real(recon(30, 1:sy)); % Rekonstruierte Pixel uebertragen
  def(1:sx, 40) = real(recon(1:sx, 40));
  def(60:65, 60:65) = real(recon(60:65, 60:65));
  def(90:95, 60:85) = real(recon(90:95, 60:85));
endfor
% Interpoliertes Bild in 'def'

Originalbild
Defektes Bild
Interpoliertes Bild

http://www.rst-software.de/dbv/download.html

Ein sehr schönes PDF hast du gemacht , nur den Code würde ich noch besser vom Text abgrenzen. Auf jeden Fall toll, dass ihr euch hier die Mühe macht.

Gregor

Dieser Artikel gefällt mir wirklich gut!

Ist eine Diskussion zu den Inhalten des Artikel mit weiteren Anregungen, Ergänzungen usw. erwünscht?

Michael E.

Auf jeden Fall

Gregor

Michael E. schrieb:

Auf jeden Fall

Ok, dann kommen hier mal ein paar Anregungen und Hinweise von mir.

Bei der hier gezeigten c++ Implementierung wird der Rand (also die Pixel, für die die Filtermaske nicht vollständig gefüllt ist) nicht gefiltert. Ein besseres Verfahren ist z.B. die fehlenden Werte mit 0 anzunehmen.

Ich wollte hier darauf hinweisen, dass man an das "Randproblem" durchaus mit vielen unterschiedlichen Ansätzen herangeht, die natürlich auch für jeweils unterschiedliche Einsatzgebiete geeignet sind. Letztendlich kann man mit den ganzen Ansätzen, die es so gibt, wahrscheinlich ganze Bücher füllen und wahrscheinlich gibt es diese Bücher auch tatsächlich. Zwei weitere Ansätze für das Randproblem sind zum Beispiel.

1. Man kann jeweils den Wert des nächsten Pixels im Bild für einen Bildpunkt auf dem Rand annehmen.

2. Man kann das Ende des Bildes als eine Art Spiegel ansehen und für einen Bildpunkt auf dem Rand jeweils den Wert des "Spiegelpixels" im Bild annehmen.

Jede Variante hat hier ganz unterschiedliche Auswirkungen auf die äußeren Bereiche des Ausgabebildes. Wenn man den Rand des Bildes überall auf 0 setzt, dann wird bei Anwendung eines Mittelwertfilters das Ausgabebild nach außen hin dunkler. Bei Anwendung eines Ableitungsfilters werden vielleicht ungewollt große Steigungen in den äußeren Bereichen des Ausgabebildes angezeigt.

Nächster Punkt: Der Gaussfilter.

An dieser Stelle empfehle ich interessierten Lesern des Artikels, sich ein bischen mehr mit der dahinterstehenden Mathematik zu befassen, da diese hier interessante Möglichkeiten bietet, mit denen man beispielsweise eine ganze Menge Performance herausholen kann. Bei einem 3x3-Gaussfilter wird man da zwar noch nicht so viel herausholen können, aber wenn man es plötzlich mit einem 11x11-Gaussfilter zu tun hat, ist es schon sinnvoll, zu wissen, dass man hier die 2-dimensionale Faltung in 2 eindimensionale Faltungen aufteilen kann. Während man dann in der zweidimensionalen Faltung 11*11=121 Multiplikationen pro Pixel zu berechnen hat und entsprechend viele Zahlen summieren muss, hat man in den zwei eindimensionalen Faltungen nur noch 2*11=22 Multiplikationen pro Pixel zu berechnen und kann nebenbei auch noch einiges an Speicher sparen, weil man den Algorithmus "in-place" machen kann und dazu nur einen relativ kleinen Buffer benötigt, der einer Zeile/Spalte des Bildes entspricht.

Ein weiterer Punkt ist hier die Möglichkeit der Kombination von Gaussfilter und Ableitung. Wenn man beides machen möchte, kann man sich einiges an Zeit sparen, wenn man statt 2 Faltungen, einmal mit einem Gaussfilter und einmal mit einem Ableitungsfilter, nur noch eine Faltung mit der Ableitung eines Gaussfilters durchzuführen hat.

Insgesamt lohnt es sich einfach, die dahinterstehende Mathematik halbwegs zu kennen, wenn man mit Faltungen, Fouriertransformationen usw. zu tun hat. Die Mathematik bietet einem an dieser Stelle viele Möglichkeiten und zeigt interessante Eigenschaften dieser Operationen auf.

freshman

Hallo,
ich verstehe zwar nur einen Bruchteil, traue mich aber trotzdem mal zu fragen.
Zum ersten Beispiel, siehe Code:

template <typename T> 
void rotate(T* din, T* dout, unsigned sx, unsigned sy, double w) 
{                        //was ist unsigned für ein Datentyp? Muß man int nicht angeben?
    for (unsigned i = 0; i < sy; ++i) 
    { 
        for (unsigned j = 0; j < sx; ++i) //wird j nicht inkrementiert?
        { 
            signed rx = (signed)((double)j*cos(w) - (double)i*sin(w)); 
            signed ry = (signed)((double)j*sin(w) + (double)i*cos(w)); 
            if (rx < 0 || ry < 0 || rx >= sx || ry >= sy) 
                continue; 
            dout[i*sx + j] = din[ry*sx + rx]; 
        } 
    } 
    return; 
}

grübel dann schon einmal weiter...

Gregor

@freshman:

1. "unsigned" ist das Gleiche wie "unsigned int".

2. Die Tatsache, dass das j nicht inkremetiert wird und stattdessen i, ist wohl ein Bug.

wie siehst aus mit´n (c) ??

Korbinian

Hoppla!
Danke für Hinweis auf den Tippfehler: Natürlich muss nicht i sondern j inkrementiert werden. Im Beispielprojekt zum download sollten allerdings keine Fehler sein.

mehr davon!

hallo zusammen,

ich hoffe ihr könnt mir helfen!

ich muß ein Kantenbild erzeugen, dasgehört zum thema Morphologe Operatoren!
dieses bild wird mit einer ausgewählte maske (entweder 3x3 oder 5x5 maske)
und auch nach einem auswahl der innere oder äußere kante.

ich hoffe, das jemeinden mir helfen kann.bitte es ist sehr wichtig und ich muß vor montag mit den Programme fertig sein.

ich freue mich auf eine schnelle antwort!

vielen dank

dEUs

Kein Mensch kapiert was du willst, wenn du deine Fragen nciht auf deutsch formulierst.

MrBurns

Ich hab das ganze nur überflogen, aber zur Optimierung des Gaussfilters ist es wohl besser den Filter zu separieren (was Gregor sagte). Dies ist immer dann möglich wenn dies gilt.
z.B.

0 1 0   0 0 0   1 1 1
0 1 0 * 1 1 1 = 1 1 1
0 1 0   0 0 0   1 1 1

oder 

0 1 0   0 0 0   1 2 1
0 2 0 * 1 2 1 = 2 4 2
0 1 0   0 0 0   1 2 1

Man hat dann nur noch zwei 1D Filter und nicht einen 2D.

Dann führt man jeweils eine Filterung des Bildes in X und eine in Y Richtung durch.

Wenn mans noch effizienter will, kopiert man die zu Filternde Zeile/Spalte in ein Array und den zusätzlichen Rand (spiegeln...) gleich mit. Dies hat den Vorteil, dass man nicht bei der Filterung prüfen muss, ob der Filter "rausragt", man spart also die ifs. Und man hat bei der Filterung in Y Richtung weniger Cache Misses, da es sehr wahrscheinlich ist, dass eine Spalte in den Cache passt, aber nicht das ganze Bild.

Korbinian

für den gaussfilter auf jeden fall, für den mittelwertfilter wäre ich mir da nicht so sicher: meine implementierung durchläuft das NxM feld genau einmal mit M*N + 2M schritten, für jeden schritt 8 additionen und zwei zuweisung. die aufspaltung würde dazu führen, das feld 2 mal im ganzen zu durchlaufen, dafür nur mit einer addition, einer subtraktion und einer zuweisung. ich habs jetz nicht exakt nachgeprüft, aber für große bilder dürft meins schneller sein, auch wenn du das bild nicht spiegelst sondern über pointer gehst.

MrBurns

Kannst du den Code mal posten.

ok mann, ich formoliere es dann anders.

so lautet dann die Aufgabe:
Erstellen Sie ein Programm zur Kantenerzeugung von Binärbildern wahlweise mithilfe einer 3x3 - oder 5x5-Maske.Man kann sog. innere und äußere Kanten erzeugen.

Das Programm soll die folgenden Anforderungen erfühllen:
=>Erzeugung wahlweise einer inneren oder äußeren Kante mit wahlweise einer 3x3- oder 5x5-Maske.
=>Darstellung des Kantenbildes.

und es gibt einen Regel zur Erzeugung einer Kanten bildes:

dilatiertes Bild XOR Quellbild = ein einpixelbreites Kantenbild
bzw.
quellbild XOR erodiertes Bild = ein einpixelbreites Kantenbild

Wenn Sie eine 5x5-Maske nehmen, dann wird die Kante breiter als ein Pixel.

ich hoffe, dass ich es dies mal besser ausgedrückt habe.
ich bedanke mich vielmals, dass du auf meine Frage geantwortet hast, ist wirklich sehr nett.

ich hoffe, dass du mich dies mal helfen könntest.
ich werde dann auf deine antwort warten.

danke nochmal .

Adil

Korbinian

MrBurns schrieb:

Kannst du den Code mal posten.

So muss mich Korrigieren, ich meinte nicht den 3x3 Mittelwert (den man durch geeignete Pointer in "linearer" zeit (MxNx(8 add, 1div, 1 zuweis) machen kann) sondern den 3x3 Gauss, und der ist oben im Artikel. Allerdings spalte ich den 3x3 Kernel in eine doppelte Anwendung eines 2x2, wodurch man besser implementie

@Adil
Erwartest du jetzt dass jemand deine Hausaufgaben macht? Das solltest du eigentlich (dir zu liebe) selber machen. Ein Tip: Im Artikel oben wird gezeigt, wie man mit einem 3x3 Filter ein Kantenbild erzeugt. Noch ein Tip: Nachdem du ein binäres bild hast vereinfacht es den Filter. Es wird dir ein Hinweis auf Dilatation und Erosion gegeben, was eigentlich nichtlineare Filter sind. Im binären allerdings kannst du das trotzdem recht schick machen, da es so aussieht:
Erosion: Wenn im Filterbereich eine 0 vorkommt, setze das aktuelle Pixel auf 0
Dilatation: Wenn im Filterbereich eine 1 vorkommt, setze das aktielle Pixel auf 1

Ersteres macht das Bild optisch kleiner (frisst was weg), letzteres gibt was dazu. Was du jetzt implementieren musst ist lediglich das abfahren des Bildes mit deiner Filtermaske und das anschliessende ver-xor-en mit dem urbild. Wie das abfahren geht, beschreibe ich oben.

Souza

servus!
Hab das Forum hier grad entdeckt und auch gleich vieles zu fragen. Und zwar muss ich für die Uni einen Mittelwertfilter programmieren. Das Problem ist, dass ich kaum mit c++ gearbeitet hab und auch sonst nicht wirklich fit bin im programmieren. Kann mir vielleicht jemand schildern, wie man in c++ ein Bild einlesen (also Pfadangabe im code) und dann den Mittelwertfilter darauf anwenden kann und dieses Bild dann in verändertem Zustand wieder ausgeben kann. Soll nämlich n Plugin für ein Grafikprogramm werden, wenns fertig ist. Soll nix fertiges sein, aber vielleicht ne Anleitung in die richtige Richtung. Allein kriege ichs nicht gebacken. Das grübeln hat kein Ende.

vielen Dank im voraus

Korbinian

An der Uni solltest du das lesen aber bereits beherrschen: Wie du einen (Mittelwert)Filter in c++ realisierst ist dort nämlich haarklein beschrieben, sowohl in Theorie als auch Praxis. Das Bildeinlesen ist etwas trickreicher, wenn du dich mit PGM (portable graymap) Bildern begnügst, kannst du aus meinem Beispielprojekt die lese und schreibfunktionen dafür verwenden. Alternativ bieten sich die verschiedenen Bibliotheken an (die du über google findest): libpng, libjpg und andere. Die einzubinden ist allerdings anfangs ein gefummel, da die oft recht umständlich sind. Wenn du noch Schwierigkeiten mit c(++) hast, würde ich empfehlen, dass du das erstmal mit leichten Tutorials aus der Welt schaffst. Wenn dir nur der Überblick fehlt, kannst du mal in mein Beispielprojekt reinsehen, wie die funkionen implementiert werden, und wie sie benutzt werden (in den Tests). Wenn du das ganze als Plugin schreiben sollst musst du dich auch noch mit den Pluginkonventionen rumärgern.

Hilft das?