Interpreterbau - Ein Anfang
-
Inhalt
- Einleitung
- Motivation
- Quellcodes
- Erklärung einiger Begriffe
- Erweiterte Backus-Naur-Form (EBNF)
- Scanner
- Parser
- Abstrakter Syntaxbaum
- Endspurt
- Abschluss
- Downloads
1 Einleitung
Die Entwicklung eines Compilers (Compilerbau oder auch Übersetzerbau) ist schon lange keine Magie mehr: Tatsächlich handelt sich um ein sehr interessantes Themengebiet in der Informatik. Trotzdem besitzt es heutzutage noch immer den Ruf, dass es für einen "normalen" Menschen nicht möglich sei, selbst einen Compiler zu entwickeln.
Als interessierter Leser stellt man sich selbstverständlich die Frage: "Warum? Woher kommt das?".
Nun, früher war eben nicht alles besser. Computer hatten nicht so viel Leistung und der Speicher war natürlich auch stark begrenzt. Und doch hat man es geschafft, effiziente Programme zu schreiben. Dazu optimierte man an vielen Stellen, lagerte Programmteile aus und betrieb tatsächlich ein bisschen kreative "Zauberei". Diese Art Optimierung trat insbesondere bei Compilern auf, da an diese besondere Leistungsanforderungen gestellt wurden. Sie erfuhren also enorme Optimierungen, so dass die Lesbarkeit und Verständlichkeit des Quellcodes dadurch immer weiter abnahm.
Warf man dann als Neugieriger einen Blick auf einen solchen Quellcode, sah man sehr komplexen, unverständlichen Code.
Doch das muss heute nicht mehr sein!
Das alles liegt inzwischen in weiter Ferne und es hat sich viel getan. So wurden nicht nur die Vorgehensweisen weiterentwickelt, vereinfacht und verfeinert. Auch die Computer sind viel leistungsfähiger geworden und wir können getrost auf solche Optimierungen verzichten.2 Motivation
Nach dieser Einleitung sollte klar geworden sein:
Auch Compiler sind letztendlich nur Computerprogramme. Wir werden uns in diesem Teil des Artikels auf die Entwicklung eines Matheparsers beschränken. Jedoch sollen damit die Grundsteine für mehr gelegt werden. Genauer gesagt soll in den weiteren Teilen dieser Artikelserie eine kleine Scriptsprache entstehen. Das dazu notwendige Wissen soll Schritt für Schritt aufgebaut werden. Dieses Wissen beschränkt sich nicht nur auf die eigentliche Programmierung, sondern soll auch zeigen wie man eine eigene Syntax definiert und später als Programm umsetzt.Auf komplizierte theoretische Erklärungen wird möglichst verzichtet.
Stattdessen gib es viele funktionsfähige Beispielcodes, die die beschriebenen Konzepte näher bringen und implementieren - die Tür für eigene Experimente ist damit geöffnet.3 Quellcodes
Ich habe mich bemüht, möglichst viel Quellcode direkt im Artikel zu zeigen. Doch natürlich kann ich nicht bei jeder kleinsten Änderung den gesamten Quellcode wiederholen. Das ist aber kein Problem, da der gesamte Quellcode als Download bereitsteht. Sollten also Unklarheiten entstehen, so kann ein Blick in den Quellcode nicht schaden.
Die in diesem Artikel verwendete Programmiersprache ist natürlich C++, aber es steht auch eine (fast) exakte Portierung in die Programmiersprache C# zur Verfügung.
Der Vorteil: Hier ist eine GUI gegeben, so dass die Funktionsweise besser visualisiert werden kann. Dabei wird sowohl das Ergebnis des Scanvorgans als auch das Ergebnis des Parsingvorgangs angezeigt. Hier kann also auch experimentiert werden.4 Erklärung einiger Begriffe
Um den Zusammenhang der einzelnen Begriffe verständlicher zu machen, folgt eine kurze Erklärung:
EBNF
Mit der EBNF (Erweiterte Backus-Naur-Form) können Grammatiken definiert werden.
Bevor eine Grammatik für eine Sprache definiert wird, muss man sich aber überlegen, wie die Sprache überhaupt aussehen soll. Hat man dies geklärt, kann man beginnen die Grammatik als EBNF darzustellen. Dabei hilft diese Notation ungemein, da aus ihr sofort ersichtlich wird, welche Funktionen später programmiert werden müssen und aus welchen "Zeichen" die Sprache besteht.Scanner
Nachdem die EBNF also aufgestellt wurde, kann ein Scanner entwickelt werden, welcher die Eingabe in kleine Teile "zerteilt". Man bezeichnet diese kleinen Teile als Tokens. Dabei wird aus der EBNF ersichtlich, welche Tokens der Scanner erkennen muss. Bei einem mathematischen Ausdruck sind das natürlich die Zahlen und Operatoren. Je nach Komplexität müssen auch noch weitere Tokens, wie z.B. Bezeichner (für Konstanten z.B.PI) aus der Eingabe extrahiert werden.Parser
Der Parser steuert schließlich den Scanner an und erfragt immer das nächste Token.
Dabei wird überprüft, ob das erhaltene Token an dieser Stelle überhaupt gültig ist. Es findet also eine Überprüfung der Syntax statt. Bei Sprachen mit Variablen, etc. findet an dieser Stelle zudem die sog. semantische Analyse statt: Es wird überprüft, ob z.B. Variablen deklariert wurden.
Durch die Möglichkeit, Funktionen rekursiv aufzurufen, kann der Parser auch verschachtelte Ausdrücke ohne Mehraufwand parsen: Er ruft einfach die Anfangsfunktion erneut auf. Um weitere Optimierungen zu ermöglichen, wird beim Parsingvorgang häufig ein Abstrakter Syntaxbaum (siehe nachfolgende Erklärung) aufgebaut.Abstrakter Syntaxbaum
Der Abstrakte Syntaxbaum ermöglicht es weitere Optimierungen durchzuführen. Auch die Codegenerierung kann so vom eigentlichen Parsing getrennt werden. Dabei stellt er das Ergebnis des Parsingvorgangs in einer baumartigen Struktur dar, die alle notwendigen Informationen beinhaltet.Das C# Programm visualisiert diesen Vorgang für einen eingegebenen Ausdruck.
5 Erweiterte Backus-Naur-Form (EBNF)
Wie bereits erwähnt kann mit der EBNF eine Syntax definiert werde.
Dazu zunächst eine kleine Übersicht über einige (es gibt noch mehr) in der EBNF verwendeten Zeichen:
[b]Alternative[/b] | [b]Optionale Wiederholung[/b] { } [b]Gruppierung[/b] ( ) [b]Option[/b] [ ]Eine Syntax kann dann beispielsweise so aussehen:
[b]Antwort[/b] = "ja" | "nein" ;Das besagt, dass das Nichtterminalsymbol (Nichtterminalsymbole stehen links) Antwort entweder "ja" oder "nein" sein kann. Alle anderen Eingaben sind ungültig.
Man kann das ganze noch in je ein eigenes Nichtterminalsymbol "auslagern":
[b]Antwort[/b] = (AntwortPositiv) | (AntwortNegativ) ; [b]AntwortPositiv = "ja"[/b] ; [b]AntwortNegativ = "nein"[/b] ;Will man nun weitere Möglichkeiten definieren, so geht das auch sehr einfach:
[b]Antwort[/b] = (AntwortPositiv) | (AntwortNegativ) ; [b]AntwortPositiv[/b] = (AntwortPositivDeutsch) | (AntwortPositivEnglisch) ; [b]AntwortPositivDeutsch[/b] = "ja" | "jo" ; [b]AntwortPositivEnglisch[/b] = "yes" | "yeah" ; [b]AntwortNegativ[/b] = (AntwortNegativDeutsch) | (AntwortNegativEnglisch) ; [b]AntwortNegativDeutsch[/b] = "nein" | "ne"; [b]AntwortNegativEnglisch[/b] = "no" | "nope";Man erkennt, dass man das ganze durch einsetzen oder "auslagern" umformen kann.
Auch Rekursionen sind möglich - wir machen davon später Gebrauch.Soll eine Syntax definiert werden, die nur Zahlen zulässt und die keine 0 enthält, so definieren wir uns zunächst ein Symbol für alle Ziffern außer 0:
[b]AlleZiffernAußerNull[/b] = "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Und das Symbol an dem unsere Syntax startet, nennen wir sprechender Weise
Start:[b]Start[/b] = (AlleZiffernAußerNull) ;Diese Syntax akzeptiert nur eine Ziffer, die nicht 0 ist. Geplant war aber eine Ziffernfolge, die keine 0 enthält.
Dazu modifizieren wir die Syntax folgendermaßen:
[b]Start[/b] = (AlleZiffernAußerNull) { (AlleZiffernAußerNull) } ;Man könnte das so lesen: Das Symbol
Startbesteht aus einer Ziffer die nicht 0 ist. Gefolgt von keiner oder mehreren Ziffern, die nicht 0 sind.Anders gesagt: Eine Zahl die keine 0 enthält.
Die Eingabe von 4453453 wäre also gültig, während die Eingabe 1234041 ungültig ist, da sie eine 0 enthält.
Um dem Ziel, einen eigenen Matheparser zu entwickeln, näher zu kommen, definieren wir nun eine Syntax, die die Addition und Subtraktion von Zahlen erlaubt.
Zunächst definieren wir, was eine Zahl ist:
[b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ; [b]Zahl[/b] = (Ziffer) { (Ziffer) } ;Eine Zahl ist also einer Ziffer, auf die optional weitere Ziffern folgen... logisch.
Jetzt definieren wir die eigentlichen Rechenoperatoren:
[b]Start[/b] = (Zahl) { ("+" | "-") (Zahl) } ;Unsere Berechnung besteht aus einer Zahl, auf die optional ein + oder – und eine weitere Zahl folgt.
Die Eingabe von 500+12-300+12-1+5 wäre also gültig. Aber auch die Eingabe von 5 ist vollkommen korrekt. Schließlich handelt es sich bei{ ("+" | "-") (Zahl) }um eine optionale Wiederholung.Natürlich möchten wir auch Multiplikationen unterstützen. Mit der richtigen Syntax ergeben sich Dinge wie Punktrechnung vor Strichrechnung automatisch.
Die gesamte Syntax sieht dann so aus:
[b]Start[/b] = [b](Multiplikation)[/b] { ("+" | "-") [b](Multiplikation)[/b] } ; [b]Multiplikation[/b] = (Zahl) { [b]("*" | "/")[/b] (Zahl) } ; [b]Zahl[/b] = (Ziffer) { (Ziffer) } ; [b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Um das Konzept zu verstehen, betrachten wir nun den Verlauf bei der Eingabe 10.
Wir befinden uns zunächst beim Symbol
Start. Anschließend begeben wir uns zum SymbolMultiplikation, danach zum SymbolZahlund abschließend zum SymbolZiffer. Jedoch werden wir die Verarbeitung von mehreren Ziffern zu einer Zahl direkt in den Scanner implementieren. Das soll in der Praxis nicht die Aufgabe unseres Parsers sein.Wir "fallen" also bis zum Ende hindurch. Daraus lässt sich für uns eine simple Regel ableiten:
Umso weiter ein Symbol in der Syntax zurückliegt, umso eher wird es erreicht.Das ist auch der Grund warum wir in
Startdie Addition/Subtraktion definieren. Dieses Symbol wird als letztes abgearbeitet. Denn vorher wird die Multiplikation abgearbeitet. So behandeln wir die Punkt- vor Strichrechnung korrekt.Doch was wäre Mathematik ohne Klammern? Klammern haben die höchste Rangfolge, also müssen sie als erstes abgearbeitet werden. Sie landen damit in unserer Definition noch weiter hinten.
Wir müssen unsere Syntax erneut modifizieren. Das könnte so aussehen:
[b]Start[/b] = (Multiplikation) { ("+" | "-") (Multiplikation) } ; [b]Multiplikation[/b] = [b](Klammer)[/b] { ("*" | "/") [b](Klammer)[/b] } ; [b]Klammer[/b] = (Zahl) | [b]"(" (Start) ")" ;[/b] [b]Zahl[/b] = (Ziffer) { (Ziffer) } ; [b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Wenn man sich das genau ansieht, stellt man fest: Wir haben eine Rekursion mit dem Symbol
Startin unserer Syntax. Diese Rekursion ist gewollt, da in einer Klammer auch z.B. wieder eine Klammer stehen kann. Damit wir auch mit Klammern und Zahlen umgehen können, vor denen ein Vorzeichen steht, müssen wir noch eine letzte kleine Änderung machen:[b]Start[/b] = (Multiplikation) { ("+" | "-") (Multiplikation) } ; [b]Multiplikation[/b] = (Klammer) { ("*" | "/") (Klammer) } ; [b]Klammer[/b] = [b]["+" | "-"][/b] ((Zahl) | "(" (Start) ")") ; [b]Zahl[/b] = (Ziffer) { (Ziffer) } ; [b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Damit kann vor einer Klammer auch ein Vorzeichen stehen, aber es muss natürlich nicht.
Unsere Syntax ist an dieser Stelle fertig. Wir haben damit die Syntax für die Grundrechenarten, sowie Klammern aufgestellt.
Auch die Rechenregeln sind berücksichtigt. Das soll uns zunächst genügen, aber natürlich wollen wir auch ein Programm entwickeln, das nach dieser Syntax vorgeht und uns aus einer Eingabe ein mathematisch korrektes Ergebnis liefern kann.Damit wir bei der Eingabe der Daten möglichst flexibel sind und z.B. Leerzeichen automatisch ignoriert werden, teilen wir unser Programm in zwei Programmteile (repräsentiert durch Klassen) auf:
- Scanner (auch Lexer genannt)
- Parser
Zum vollständigen Verständnis ist es sehr wichtig, dass dieser Teil des Artikels (EBNF) gut verstanden wird. Eine gute Übung wäre es z.B. die Syntax für mathematische Terme selbst noch mal aufzustellen. Auch das manuelle anwenden auf einen mathematischen Term (angefangen von 5+5 bis 100 * 3 + (4 - 1 * )) mit Stift und Papier wäre für das Verständnis vielleicht förderlich.
6 Scanner
Der Scanner "zerteilt" die Eingabe in sogenannte Tokens. Der Parser ruft diese Tokens nach und nach vom Scanner ab und verarbeitet sie nach der von uns aufgestellten Syntax. Dabei bereinigt der Scanner die Eingabe auch von allen unerwünschten Zeichen, zum Beispiel Leerzeichen, Tabulatoren und auch Zeilenumbrüchen.
Wir beginnen nun mit der Programmierung des Scanners. Als erstes benötigen wir eine Enumeration mit den möglichen Typen von Tokens, damit wir diese unterscheiden können:
// Unsere Arten von Tokens enum TokenType { TT_PLUS, // + TT_MINUS, // - TT_MUL, // * TT_DIV, // / TT_LPAREN, // ( TT_RPAREN, // ) TT_NUMBER, // 12345 TT_NIL // NIL (=Not In List) => Kein passendes Token gefunden };Damit wir später auch eine verständliche Fehlermeldung ausgeben können, legen wir noch ein Array an, das die Namen der Tokens als Zeichenfolge hält:
// Unsere Arten von Tokens als String (Für Fehlermeldungen) static const char *TokenTypeStr[] = { "TT_PLUS", "TT_MINUS", "TT_MUL", "TT_DIV", "TT_LPAREN", "TT_RPAREN", "TT_NUMBER", "TT_NIL" };Das Präfix TT_ steht hier für TokenType. Mit dieser Aufzählung können wir unsere Tokens unterscheiden. Dem TokenType
TT_NILkommt dabei eine ganz besondere Bedeutung zu: Sollte der Scanner das Ende der Eingabe erreicht haben oder kein Token erkennen, so bezeichnen wir dieses alsTT_NIL.Damit wir einem Token auch einen Wert zuweisen können (eine erkannte Zahlenfolge hat schließlich auch einen Zahlenwert) schreiben wir uns eine Klasse
Token, in der wir neben dem TokenType auch den Wert speichern können:class Token { private: TokenType myType; int myValue; public: Token(TokenType type = TT_NIL, int value = 0); TokenType getType() const { return myType; } int getValue() const { return myValue; } // Für Fehlermeldungen const char *toString() const { return TokenTypeStr[myType]; } // Zum Vergleichen bool equal(TokenType type) const { return myType == type; } };Nehmen wir nun als Beispiel die Eingabe 10+3.
Es handelt sich dabei um folgende Tokens:
TT_NUMBERmit einem Wert von 10
TT_PLUSmit einem Wert von 0 (Standardwert. Schließlich braucht das Plus keinen Wert)
TT_NUMBERmit einem Wert von 3Diese "Zerteilung" ist die Aufgabe unseres Scanners, der dazu eine Funktion
getNextTokenanbieten soll. Dabei wird die Eingabe Zeichenweise gelesen.
Wird zum Beispiel das Zeichen + gelesen, so wird das TokenTT_PLUSangenommen und von der Funktion zurückgegben. Wird die Ziffer 1 gelesen, so wird so lange weitergelesen, bis keine Ziffer mehr folgt und die gesamte Zahl als TokenTT_NUMBERzurückgegeben.Auf diese Weise können wir unsere Eingabe für den Parser in Tokens verarbeiten, überflüssige Zeichen ignorieren und Fehlermeldungen ausgeben, falls unbekannte Zeichen auftreten.
Damit haben wir erst mal das Wichtigste zusammen und können uns nun an den Scanner wagen. Dabei handelt es sich auch um eine Klasse, die zunächst die Eingabe als
std::stringspeichert. Außerdem weiß sie darüber Bescheid, an welcher Stelle wir uns in der Eingabe zurzeit befinden und welches Zeichen wir zuletzt gelesen haben.Außerdem enthält die Klasse die angesprochene Funktionen
getNextToken, sowieskipSpacesundreadNextChar. Auf deren Implementierung und Sinn wird im Folgenden noch genauer eingegangen.Doch zunächst die Klasse
Scanner, welche - für viele vielleicht überraschend - erstaunlich klein ausfällt:class Scanner { private: std::string myInput; unsigned int myPos; // Aktuelle Position in der Eingabe char myCh; // Zuletzt gelesenes Zeichen public: Scanner(const std::string& input); Token getNextToken(); private: void skipSpaces(); void readNextChar(); };Als erstes betrachten wir die Funktion
readNextChar. Wie der Name bereits vermuten lässt, liest diese Funktion das nächste Zeichen ein. Das ist zwar sehr simpel, aber man muss hierbei natürlich beachten, dass man nicht mehr liest, als die Eingabe lang ist:void Scanner::readNextChar() { // Am Ende der Eingabe angelangt? if (myPos > myInput.length()) { myCh = 0; return; } myCh = myInput[myPos++]; }Wenn das Ende der Eingabe erreicht wurde, wird das aktuelle Zeichen auf 0 gesetzt. Das ist für uns ein eindeutiges Merkmal, dass wir das Ende erreicht haben.
Eine weitere wichtige Funktion ist die Funktion
skipSpaces. Diese Funktion sorgt dafür, dass Leerräume jeder Art (Leerzeichen, Tabulatoren, Zeilenumbrüche) ignoriert bzw. übersprungen werden:void Scanner::skipSpaces() { while (myCh == ' ' || myCh == '\t' || myCh == '\r' || myCh == '\n') { readNextChar(); } }Damit der Scanner auch anfangen kann zu arbeiten, müssen im Konstruktor noch einige Variablen initialisiert und das erste Zeichen eingelesen werden:
Scanner::Scanner(const std::string& input) : myInput(input), myPos(0) // Initialisierung { // Erstes Zeichen einlesen readNextChar(); }Jetzt ist der Scanner bereit und es folgt das Herz unseres Scanners: Die Funktion
getNextToken. Man kann den hier vorgestellten Scanner natürlich auf viele verschiedene Arten implementieren. Unter anderem wäre es denkbar, dass man zunächst alle Tokens einliest. Das kann wichtig sein, wenn man nachzusehen möchte/muss, was das nächstfolgende Token ist, ohne es tatsächlich zu lesen. Für uns ist das an dieser Stelle aber nicht relevant und wir lesen erst beim Aufruf der FunktiongetNextTokendie nächsten Zeichen ein und nicht vorher. Die andere Möglichkeit wird später aber auch noch vorgestellt.Die konkrete Funktionsweise ist sehr einfach zu verstehen. Zunächst werden alle Zeichen übersprungen, die für uns unwichtig sind. Das übernimmt die Funktion
skipSpaces. Anschließend betrachten wir das aktuelle Zeichen und entscheiden anhand von diesem Zeichen, wie damit umzugehen ist. Ist das Zeichen ein +, dann ist die Sache sofort klar: Es handelt sich um das TokenTT_PLUS. Lesen wir eine Ziffer ein, dann müssen wir überprüfen, ob noch weitere Ziffern folgen und diese zu einer Zahl zusammenfassen. Der Einfachheit wird dafür ein Buffer vom Typstd::stringverwendet. Die Ziffernfolge wird dann einfach mitatoiin eine Zahl konvertiert:Token Scanner::getNextToken() { std::string buf; // Überflüssige Zeichen ignorieren skipSpaces(); switch (myCh) { case '+': readNextChar(); return Token(TT_PLUS); case '-': readNextChar(); return Token(TT_MINUS); case '*': readNextChar(); return Token(TT_MUL); case '/': readNextChar(); return Token(TT_DIV); case '(': readNextChar(); return Token(TT_LPAREN); case ')': readNextChar(); return Token(TT_RPAREN); case '0': case '1': case '2': case '3': case '4': case '5': case '6': case '7': case '8': case '9': // Einlesen, solange es eine Ziffer ist while (isdigit(myCh)) { buf += myCh; readNextChar(); } // Der Einfachheit haben wir die Zahl zunächst in einen String eingelesen // Dieser wird nun in ein Integer konvertiert return Token(TT_NUMBER, atoi(buf.c_str())); default: if (myCh != 0) { std::cerr << "Error: nicht unterstuetztes Zeichen '" << myCh << "'" << std::endl; } break; } // Es wurde kein passendes Token gefunden. Mögliche Gründe dafür: // - Eingabe enthält kein weiteres Zeichen mehr (Ende erreicht) // - Eingabe besteht aus nicht unterstützten Zeichen return Token(TT_NIL); }Hinweis: Einige Computerprogramme akzeptieren keine Zahlen mit führenden Nullen. Die Zahlenfolge 001 wäre also ungültig und nur die Zahlenfolge 1 korrekt. Unser Scanner akzeptiert jedoch auch Zahlen mit führenden Nullen!
An dieser Stelle ist der Scanner fertig. Er kann in einem Testlauf sehr einfach getestet werden:
#include <iostream> #include <string> #include "Scanner.h" int main() { std::string input = "10 + 5\n * \t10-\n5\t"; std::cout << "Eingabe: \"" << input << "\"\n" << std::endl; Scanner scanner(input); Token tok = scanner.getNextToken(); while (!tok.equal(TT_NIL)) { std::cout << tok.toString() << " = " << tok.getValue() << std::endl; tok = scanner.getNextToken(); } }Die Ausgabe sollte sein:
Eingabe: "10 + 5
* 10-
5 "TT_NUMBER = 10
TT_PLUS = 0
TT_NUMBER = 5
TT_MUL = 0
TT_NUMBER = 10
TT_MINUS = 0
TT_NUMBER = 5Man erkennt vielleicht erst hier, welchen Vorteil wir jetzt tatsächlich haben.
Der Scanner hat sich trotz der ganzen Leerräumen nicht von seiner Aufgabe abbringen lassen und konnte die Eingabe ordnungsgemäß in seine Tokens zerlegen.Möglicherweise fragt man sich an dieser Stelle: "Wozu dieser Aufwand?"
Tatsächlich ist der Scanner ohne Parser für uns vollkommen nutzlos und bringt uns nicht weiter. Zusammen bilden sie jedoch ein perfektes Team.
Also auf zum Parser!
7 Parser
Der Scanner hat unsere Eingabe in Tokens zerlegt, was macht also nun der Parser damit?
Vereinfacht gesagt überprüft er, ob die Reihenfolge der Tokens überhaupt Sinn macht. Oder er bildet einen Abstrakten Syntaxbaum. Dazu aber später mehr, keine Sorge.
So ist die Eingabe von 5 + 5 also vollkommen korrekt, während die Eingabe von + 5 5 laut unserer Syntax keinen Sinn macht und somit ungültig ist.
Auch der Aufbau des Parsers ist sehr einfach. Er enthält als Member den Scanner und das aktuelle Token. Des Weiteren enthält er die Funktion
acceptundgetNextToken.Und natürlich enthält er noch die Funktionen, die wir aus der EBNF konstruieren können. Dazu eine kurze Erklärung. Man erinnere sich zurück:
[b]Start[/b] = (Multiplikation) { ("+" | "-") (Multiplikation) } ; [b]Multiplikation[/b] = (Klammer) { ("*" | "/") (Klammer) } ; [b]Klammer[/b] = ["+" | "-"] ((Zahl) | "(" (Start) ")") ; [b]Zahl[/b] = (Ziffer) { (Ziffer) } ; [b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Der Parser enthält die Funktionen
start,multiplikation,klammer,zahl. Wir finden diese Namen auf der linken Seite der EBNF wieder. Das ist kein Zufall, sondern der Trick an der ganzen Sache!
Das was auf der rechten Seite steht, lässt sich dann später durch entsprechende Sprackonstrukte (Schleifen, Abfragen, etc.) realisieren. Der Rückgabewert dieser Funktionen ist ein int. Damit wird der Wert des Ausdrucks zurückgegeben.Und schlussendlich gibt es noch die Funktion
parse, die den gesamten Prozess starten soll.Die Funktion
zifferbrauchen wir allerdings nicht, da diese Aufgabe bereits durch den Scanner übernommen wurde. Er hat mehrere Ziffern zu einer Zahl zusammengefasst.Die oben genannten Funktionen geben alle einen Integer als Wert zurück: Das Ergebnis unserer Eingabe. Auf Fließkommazahlen wurde hier verzichtet, aber wir werden das später noch ändern, versprochen.
Der Aufbau der Klasse
Parser:class Parser { private: Scanner myScanner; Token myTok; // Zuletzt gelesenes Token public: Parser(const std::string& input); int parse(); private: int start(); int multiplikation(); int klammer(); int zahl(); void accept(TokenType type); void getNextToken(); };Wir beginnen mit der Besprechung der Funktion
getNextToken, die einfacher nicht sein könnte:void Parser::getNextToken() { // Nächstes Token "abholen" myTok = myScanner.getNextToken(); }Die Funktion
acceptüberprüft, ob es sich um das korrekte Token handelt und gibt im Fehlerfall eine Fehlermeldung aus. Anschließend wird das nächste Token eingelesen:void Parser::accept(TokenType type) { // Stimmt das Token mit dem erwarteten überein? if (!myTok.equal(type)) { std::cerr << "Error: unerwartetes Token " << myTok.toString() << ", " << TokenTypeStr[type] << " erwartet" << std::endl; } // Wir akzeptieren das Token auch im Fehlerfall, um weitere Fehler finden zu können getNextToken(); }Der Konstruktor vom Parser muss, ähnlich wie der Scanner, zunächst seine Member initialisieren und das erste Token einlesen:
Parser::Parser(const std::string& input) : myScanner(input) // Scanner initialisieren { // Erstes Token vom Scanner abholen getNextToken(); }Die einzige Funktion, die public ist, ist die Funktion
parse.Sie startet den gesamten Parsing-Prozess:
int Parser::parse() { // Wir beginnen bei unserem Startsymbol Start int res = start(); // Nun sollten alle Tokens abgearbeitet sein und TT_NIL das Ende der Eingabe bestätigen accept(TT_NIL); return res; }Man sieht hier bereits den Einsatz von
accept. War die Eingabe korrekt darf nach Abarbeitung aller Tokens kein Token mehr übrig sein. Es sollte alsoTT_NILzurückgegeben werden.Die Funktion
startist Teil unserer Syntax und die Implementierung dieser Funktion hält sich an die aufgestellte EBNF:// Start = (Multiplikation) { ("+" | "-") (Multiplikation) } ; int Parser::start() { // (Multiplikation) int res = multiplikation(); // { ("+" | "-") while (myTok.equal(TT_PLUS) || myTok.equal(TT_MINUS)) { switch (myTok.getType()) { case TT_PLUS: getNextToken(); res += multiplikation(); // (Multiplikation) break; case TT_MINUS: getNextToken(); res -= multiplikation(); // (Multiplikation) break; } } // } return res; }Wir sehen, dass die Wiederholung (in der EBNF die geschweiften Klammern) durch eine While-Schleife realisiert ist, die solange ausgeführt wird, wie das Token
TT_PLUSoder (in der EBNF das Zeichen | )TT_MINUSist.
Und das Symbol für die Multiplikation wird durch eine weitere Funktion dargestellt, die wir einfach aufrufen.Ein kleiner Tipp am Rande: Sollten noch Verständnisprobleme da sein, kann man den Code auch einfach um ein paar Ausgaben erweitern, die hoffentlich den Programmablauf noch verständlicher machen.
Als nächstes folgt die Implementierung der Funktion
multiplikation, die vom Aufbau identisch ist:// Multiplikation = (Klammer) { ("*" | "/") (Klammer) } ; int Parser::multiplikation() { int res = klammer(); while (myTok.equal(TT_MUL) || myTok.equal(TT_DIV)) { switch (myTok.getType()) { case TT_MUL: getNextToken(); res *= klammer(); break; case TT_DIV: getNextToken(); res /= klammer(); break; } } return res; }Als fast letzter Schritt folgt die Funktion
klammer. Zunächst der Code, auf den ich dann genauer eingehe:// Klammer = ["+" | "-"] ((Zahl) | "(" (Start) ")") ; int Parser::klammer() { int sign = 1; // Für Vorzeichen (Standard: positives Vorzeichen) // Haben wir ein Vorzeichen? if (myTok.equal(TT_PLUS) || myTok.equal(TT_MINUS)) { if (myTok.equal(TT_MINUS)) { sign = -1; // Negatives Vorzeichen } getNextToken(); } // Haben wir eine Klammer? if (myTok.equal(TT_LPAREN)) { accept(TT_LPAREN); int res = sign * start(); // Rekursion accept(TT_RPAREN); return res; } // Keine Klammer, also gehen wir von einer Zahl aus return sign * zahl(); }Wir werfen wieder einen Blick auf die EBNF und vergleichen den Quellcode damit.
Man erkennt, dass wir als erstes das optionale Vorzeichen (+ und -) bearbeiten müssen. Dazu gibt es die Variablesign, die standardmäßig von einem positiven Vorzeichen ausgeht. Sollte das Vorzeichen negativ sein wirdsignauf -1 gesetzt. Anschließend überprüfen wir, ob wir eine geöffnete Klammer vorfinden. Wenn das so ist, dann rufen wir nochmalsstartauf.
Das Ergebnis vonstartwird mit der Variablesignmultipliziert. Hatten wir also ein - vor der Klammer, so wird das Ergebnis der Klammer mit -1 multipliziert und wir erhalten das korrekte Ergebnis. Durch die Rekursion lassen sich auch ineinander verschachtelte Klammern korrekt auflösen.Wenn wir keine Klammer vorgefunden haben, dann gehen wir davon aus, dass es sich um eine Zahl handeln muss und rufen die Funktion
zahlauf. Die Funktion überprüft, ob es sich um eine Zahl handelt und gibt das Ergebnis zurück. Da wir auch negative Zahlen erlauben, wird auch dieses Ergebnis mitsignmultipliziert. Damit sind Eingaben wie -5 möglich.Die Implementierung der Funktion
zahl:// Zahl = (Ziffer) { (Ziffer) } ; // Wir erhalten die gesamte Zahl vom Scanner: // Es ist also keine Zusammensetzung einzelner Ziffern zu einer Zahl nötig! int Parser::zahl() { int res = myTok.getValue(); accept(TT_NUMBER); return res; }Damit ist der Parser tatsächlich fertig!
Die Verwendung des Parsers könnte so aussehen:
#include <iostream> #include "Parser.h" int main() { std::string input; while (true) { std::cout << "Eingabe: "; std::getline(std::cin, input); Parser p(input); std::cout << "Ergebnis: " << p.parse() << "\n" << std::endl; } }Hier ein paar Beispieleingaben und die Ausgaben:
Eingabe: 10 * 5
Ergebnis: 50Eingabe: -4 + 5
Ergebnis: 1Eingabe: (10 + 5) - 3 * (2 - (10 / 5) * 2) - 100
Ergebnis: -79Eingabe: ((((-100))))
Ergebnis: -100Eingabe: ((((-100)+1)+1)+1)
Ergebnis: -97Eingabe: ((((-100)+1)+1)+1) * (40-2)
Ergebnis: -3686Eingabe: -((((-100)+1)+1)+1) * (40-2)
Ergebnis: 3686Eingabe: -(-(-(+(-100)))
Error: unerwartetes Token TT_NIL, TT_RPAREN erwartet
Ergebnis: 100Eingabe: -(-(-(+(-100))))
Ergebnis: 100War doch nicht so schwer, oder? Wie wäre es, wenn unser kleines Programm in der Lage wäre die Eingabe in C++ Code zu verwandeln? Ich stelle mir das so vor:
std::cout << [b]ADD[/b]([b]MUL[/b](5, 10), [b]SUB[/b](5, 3)) << std::endl;Das macht natürlich keinen großen Sinn, aber ist eine nette Spielerei und man kann ganz genau sehen, wie die Rechnungen intern aufgelöst wurden. Außerdem möchte ich mit dieser kleinen Idee den sogenannten Abstrakten Syntaxbaum einführen.
8 Abstrakter Syntaxbaum
Was ist ein Abstrakter Syntaxbaum überhaupt? Wie der Name verrät, handelt es sich um eine baumartige Datenstruktur.
Das könnte zum Beispiel so aussehen:
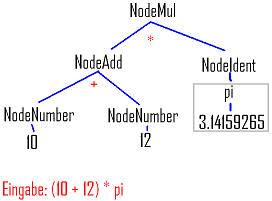
Ein solcher Abstrakter Syntaxbaum hat den Vorteil, dass wir Optimierungen vornehmen oder weitere Funktionen nachträglich einfacher hinzufügen können. Er lässt sich in C++ sehr einfach mittels Vererbung aufbauen. Allerdings müssen wir bei der Speicherreservierung und Freigabe gut aufpassen. Das wird nämlich vermehrt notwendig werden.
Wir brauchen als erstes eine abstrakte Basisklasse, die wir an dieser Stelle
Nodenennen:// Basisklasse class Node { public: virtual ~Node() { } // Ergebnis berechnen virtual int eval() const = 0; };Die Funktion
evalsoll später das Ergebnis der Rechnung zurückgeben.Die Funktion zur Codegenerierung werden wir erst später programmieren. Denn zunächst wollen wir nur, dass das Programm das gleiche macht, wie vorher. Aber eben unter Verwendung eines Abstrakten Syntaxbaums.
Jetzt benötigen wir noch eine Klasse, die eine Zahl repräsentiert und von
Nodeabgeleitet ist. Auch das lässt sich einfach realisieren:class NodeNumber : public Node { private: int myVal; public: NodeNumber(int val) : myVal(val) { } virtual int eval() const { return myVal; } };Zur Realisierung der Rechenoperationen brauchen wir jetzt noch 4 weitere Klassen:
NodeAdd,NodeSub,NodeMulundNodeDiv.Ich gebe an dieser Stelle nur
NodeAddan, da die anderen 3 Klassen einen identischen Aufbau haben und sich nur in der Rechnung unterscheiden:class NodeAdd : public Node { private: Node *myNodeLeft; Node *myNodeRight; public: NodeAdd(Node *left, Node *right) : myNodeLeft(left), myNodeRight(right) { } virtual ~NodeAdd() { delete myNodeLeft; delete myNodeRight; } virtual int eval() const { return myNodeLeft->eval() + myNodeRight->eval(); } };Man kann das auch exemplarisch austesten, wie das später funktionieren soll:
Node *node = new NodeAdd(new NodeAdd(new NodeNumber(5), new NodeNumber(10)), new NodeNumber(10)); // Speicher anfordern ... std::cout << node->eval() << std::endl; delete node; // ... und wieder freigeben!Schreibt man den Quellcode etwas einfacher, dann würde es so aussehen und man erkennt das Prinzip des Aufbaus:
[b]ADD[/b]([b]ADD[/b](5, 10), 10)Die Rechnung geht dabei von innen nach außen und stellt diese Rechenaufgabe dar:
(5 + 10) + 10Der Baum soll von unserem Parser natürlich selber aufgebaut werden. Wir müssen dazu leider einige Änderungen an unserem Parser vornehmen, aber es lohnt sich!
So ändern sich natürlich die Rückgabewerte der Funktionen. Und auch die Implementierung ändert sich. Beispielsweise sieht die Funktion
parsedann so aus:Node *Parser::parse() { // Wir beginnen bei unserem Startsymbol Start Node *res = start(); // Nun sollten alle Tokens abgearbeitet sein und TT_NIL das Ende der Eingabe bestätigen accept(TT_NIL); return res; }Die Funktion
starthat sich auch verändert. Wir rechnen das Ergebnis nun nicht mehr direkt aus, sondern legen mitnewdie entsprechenden Klassen an, die das Ergebnis durch den Aufruf vonevalausrechnen:// Start = (Multiplikation) { ("+" | "-") (Multiplikation) } ; Node *Parser::start() { Node *res = multiplikation(); while (myTok.equal(TT_PLUS) || myTok.equal(TT_MINUS)) { switch (myTok.getType()) { case TT_PLUS: getNextToken(); res = new NodeAdd(res, multiplikation()); break; case TT_MINUS: getNextToken(); res = new NodeSub(res, multiplikation()); break; } } return res; }Die Funktion
multiplikationgebe ich hier nicht an, da sie fast identisch aufgebaut ist.Die Funktionen
klammerundzahlhaben sich wie folgt geändert:// Klammer = ["+" | "-"] ((Zahl) | "(" (Start) ")") ; Node *Parser::klammer() { int sign = 1; // Für Vorzeichen (Standard: positives Vorzeichen) // Haben wir ein Vorzeichen? if (myTok.equal(TT_PLUS) || myTok.equal(TT_MINUS)) { if (myTok.equal(TT_MINUS)) { sign = -1; // Negatives Vorzeichen } getNextToken(); } // Haben wir eine Klammer? if (myTok.equal(TT_LPAREN)) { accept(TT_LPAREN); Node *res = new NodeMul(new NodeNumber(sign), start()); // Rekursion accept(TT_RPAREN); return res; } // Keine Klammer, also gehen wir von einer Zahl aus return new NodeMul(new NodeNumber(sign), zahl()); } // Zahl = (Ziffer) { (Ziffer) } ; // Wir erhalten die gesamte Zahl vom Scanner: // Es ist also keine Zusammensetzung einzelner Ziffern zu einer Zahl nötig! NodeNumber *Parser::zahl() { int res = myTok.getValue(); accept(TT_NUMBER); return new NodeNumber(res); }Man sieht, wir haben die Multiplikation mit der Variable
sign(für Vorzeichen) unter Verwendung der KlasseNodeMulundNodeNumberrealisiert. Man könnte an dieser Stelle abfragen, obsignpositiv ist und diese Multiplikation weglassen, da sie überflüssig ist, wennsign1 ist. Aber das lösen wir später anders, um eine mögliche Optimierung bei der Codegenerierung zu demonstrieren.Jedenfalls haben wir damit den Parser auf einen Abstrakten Syntaxbaum umgestellt. Wir müssen natürlich noch eine letzte Änderung in der Hauptfunktion vornehmen:
// ... // Baum generieren (Achtung: Speicher freigeben nicht vergessen!) Node *node = p.parse(); std::cout << "Ergebnis: " << node->eval() << "\n" << std::endl; // Speicher freigeben delete node; // ...Wir haben daraus noch keinen Vorteil gewonnen, aber das soll sich jetzt ändern.
Geplant war ja, dass wir die Möglichkeit bieten, C++ Code zu generieren. Dazu erweitern wir unsere Basisklasse
Nodeum folgende Funktion:virtual void generateCode(std::stringstream& strm) = 0;Diese Funktion muss nun von allen abgeleiteten Klassen implementiert werden. Und das ist keine große Sache.
Für die Klasse
NodeNumber:virtual void generateCode(std::stringstream& strm) { strm << myVal; }Für die Klasse
NodeAdd:virtual void generateCode(std::stringstream& strm) { strm << "ADD( "; myNodeLeft->generateCode(strm); strm << ", "; myNodeRight->generateCode(strm); strm << " )"; }Man sieht, wir rufen für die entsprechenden Nodes auch die Funktion
generateCodeauf, die sie wieder für ihre Nodes aufrufen. Dadurch wird immer weiter anstrmangehangen bis alles abgearbeitet wurde.Die Funktion
generateCodesieht für die KlassenNodeSub,NodeMulundNodeDivgenau so aus, nur mit dem Unterschied, dass dort SUB, MUL bzw. DIV verwendet wird.Damit wir auch einen gültigen Quellcode erhalten, müssen wir uns noch um das Drumherum kümmern. Da die Funktion
generateCodeimmer anfügt, müssen wir sowohl vor dem Aufruf als auch nach dem Aufruf, die benötigen Zeilen anfügen, um ein gültiges C++ Programm zu erhalten.Wir lagern diesen Teil in einer eigenen Funktion aus:
void generateCode(Node *node, std::stringstream& strm) { // Codegerüst (anfang) strm << "#include <iostream>\n\n" << "#define ADD(x, y) ((x) + (y))\n" << "#define MUL(x, y) ((x) * (y))\n" << "#define SUB(x, y) ((x) - (y))\n" << "#define DIV(x, y) ((x) / (y))\n\n" << "int main()\n" << "{\n" << "\tint res = "; // Den generierten Code vom Parser anhängen node->generateCode(strm); // Codegerüst (ende) strm << " ;\n\n" << "\tstd::cout << res << std::endl;\n" << "\treturn 0;\n" << "}\n"; }Und die rufen wir dann ganz einfach auf:
Parser p(input); // Baum generieren (Achtung: Speicher freigeben nicht vergessen!) Node *node = p.parse(); std::cout << "\nErgebnis: " << node->eval() << "\n" << std::endl; std::stringstream strm; generateCode(node, strm); // <---------- // Speicher freigeben delete node; std::cout << strm.str() << std::endl;Gibt man nun 100 + 5 * 3 - 4 ein, sollte folgender Code generiert werden:
#include <iostream> #define ADD(x, y) ((x) + (y)) #define MUL(x, y) ((x) * (y)) #define SUB(x, y) ((x) - (y)) #define DIV(x, y) ((x) / (y)) int main() { int res = SUB( ADD( MUL( 1, 100 ), MUL( MUL( 1, 5 ), MUL( 1, 3 ) ) ), MUL( 1, 4 ) ) ; std::cout << res << std::endl; return 0; }Hier können wir optimieren: Beispielsweise fällt die dauernde Multiplikation mit 1 auf. Sie ist durch die Multiplikation mit
signentstanden.
Wir wollen nur dann den rechtenNodeauswerten, falls der linkeNode1 ergibt. Dazu prüfen wir zunächst, ob es sich überhaupt um ein NodeNumber handelt. Das ist nur deshalb notwendig, daevalansonsten den gesamten Ausdruck auswertet. Wir wollen ja später noch etwas für den C++ Compiler übrig haben. Beispiel:(4 - (2+1)) * 2Würden wir hier
evalaufrufen, würde die gesamte linke Klammer vollständig ausgerechnet und wegoptimiert, da sie 1 ergibt. Das wollen wir aber nicht.Wir wollen nur optimieren, falls dort bereits eine 1 steht:
1 * 42Da wir keine Unterscheidungsmöglichkeit für die Nodes haben, nutzen wir für diese kleine Sache
typeidund überprüfen so, ob es sich um eine Zahl handelt:virtual void generateCode(std::stringstream& strm) { if (typeid(*myNodeLeft) == typeid(NodeNumber) && myNodeLeft->eval() == 1) { myNodeRight->generateCode(strm); } else { strm << "MUL( "; myNodeLeft->generateCode(strm); strm << ", "; myNodeRight->generateCode(strm); strm << " )"; } }Probieren wir nun die gleiche Rechnung nochmal, erhalten wir:
#include <iostream> #define ADD(x, y) ((x) + (y)) #define MUL(x, y) ((x) * (y)) #define SUB(x, y) ((x) - (y)) #define DIV(x, y) ((x) / (y)) int main() { int res = SUB( ADD( 100, MUL( 5, 3 ) ), 4 ) ; std::cout << res << std::endl; return 0; }Man sieht, dass die unnötigen Multiplikationen weggefallen sind.
Wir wollen diesen Ausdruck als kleines Beispiel ausrechnen. Dafür beginnen wir ganz innen und bewegen uns immer weiter nach außen.
SUB( ADD( 100, [b]MUL( 5, 3 )[/b] ), 4 )Zunächst berechnen wir die Multiplikation. Das Ergebnis von 5 * 3 ist 15.
Wir setzen also 15 ein:
SUB( [b]ADD( 100, [u]15[/u] )[/b], 4 )Die nächst innere Berechnung ist die Addition.
Wir rechnen also 100 + 15 aus und setzen wieder ein:
SUB( [u]115[/u], 4 )Schlussendlich subtrahieren wir 115 von 4 und erhalten das finale Ergebnis 111.
Wenn der Parser einfach mal herausgefordert werden soll, kann man folgende Rechnung berechnen lassen.
Das Ergebnis müsste 6990 sein:
(10 + 5) - 3 * (2 - (10 / 5) * 2) - 100 -((((-100)+1)+1)+1) * (40-2) + ((((-100)+1)+1)+1) - (10 + 5) - 3 * (2 - (10 / 5) * 2) - 100 -((((-100)+1)+1)+1) * (40-2) + ((((-100)+1)+1)+1)
Interessant ist natürlich auch der dafür generierte C++ Code:
int res = ADD( SUB( SUB( SUB( SUB( ADD( SUB( SUB( SUB( ADD( 10, 5 ),
MUL( 3, SUB( 2, MUL( DIV( 10, 5 ), 2 ) ) ) ), 100 ),
MUL( ADD( ADD( ADD( MUL( -1, 100 ), 1 ), 1 ), 1 ),
SUB( 40, 2 ) ) ), ADD( ADD( ADD( MUL( -1, 100 ), 1 ), 1 ),1 ) ),
ADD( 10, 5 ) ), MUL( 3, SUB( 2, MUL( DIV( 10, 5 ), 2 ) ) ) ), 100 ),
MUL(ADD( ADD( ADD( MUL( -1, 100 ), 1 ), 1 ), 1 ),
SUB( 40, 2 ) ) ), ADD( ADD( ADD(MUL( -1, 100 ), 1 ), 1 ), 1 ) ) ;Damit es keine Fehler gibt, muss man immer aufpassen, dass der entstandene Code bei der Ausgabe (Konsolenfenster) nicht durch die Limitierung von Zeilenlängen ungünstig getrennt (z.B. zwischen zwei Ziffern) und damit falsch kopiert wird.
9 Endspurt
Der Matheparser funktioniert zwar, aber er ist noch etwas funktionsarm. Außerdem gibt es noch ein paar Schwächen auszubessern. Unter anderem sollen endlich Fließkommazahlen unterstützt werden. Außerdem sollen Funktionen und Konstanten ermöglicht werden.
Wir werden dazu große Teile des Codes verwerfen müssen, aber das ist es natürlich mal wieder wert. Auch ist es ein Beweis dafür, dass man ganz am Anfang alles einplanen sollte, da es später nicht mehr so einfach möglich ist.
Wir beginnen also wieder ganz vorne mit einer neuen EBNF:
[b]Start[/b] = (Multiplikation) { ("+" | "-") (Multiplikation) } ; [b]Multiplikation[/b] = (Klammer) { ("*" | "/") (Klammer) } ; [b]Klammer[/b] = ["+" | "-"] ([b](Funktion) | (Bezeichner)[/b] | (Zahl) | "(" (Start) ")") ; [b]Funktion[/b] = (Bezeichner) '(' [ (Start) { ',' (Start) } ] ')' ; [b]Bezeichner[/b] = ( ('a' - 'Z') | '_' ) { ('a' - 'Z') | '_' } ; [b]Zahl[/b] = (Ziffer) [ '.' ] { (Ziffer) } ; [b]Ziffer[/b] = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" ;Diese EBNF ähnelt offensichtlich der am Anfang aufgestellten, wurde jedoch um Konstanten und Funktionen erweitert. Außerdem werden Fließkommazahlen unterstützt. Ein
Bezeichnerbesteht aus einem Zeichen, gefolgt von beliebig vielen weiteren Zeichen oder einem Unterstrich.Wir stoßen jedoch auf ein Problem. Nehmen wir folgende Eingaben:
PI + 10sin(10)Beim Parsen der ersten Eingabe, weiß der Parser nicht, ob nach dem Bezeichner
PInoch eine öffnende Klammer kommt, wie in der zweiten Eingabe.Das ist nicht gut, aber ich erwähnte ja anfangs bereits, dass man den Scanner auch anders konzipieren kann. Wir wollen die Gelegenheit nutzen und ihn für diese Situation (um)rüsten.
Die Idee ist zunächst folgende: Wir füllen einen
std::vectormit allen Tokens. Wir können uns dann frei in dieser Liste bewegen und so entscheiden, wie das folgende Token aussieht.Wir benennen unsere alte Funktion
getNextTokenzunächst inreadNextTokenum, und machen sieprivate.
Sie wird später nur noch zur Füllung der Liste genutzt.Dann erstellen wir eine neue Funktion
getNextTokenmit einem Parameterpeekder den Standardwertfalseerhält.Außerdem benötigen wir den besagten Vector und eine Positionsangabe, damit wir wissen, wo wir uns befinden.
Das sollte dann insgesamt so aussehen:
typedef std::vector<Token> TokenVec; class Scanner { private: std::string myInput; unsigned int myPos; // Aktuelle Position in Eingabe unsigned int myVecPos; char myCh; // Aktuelles Zeichen TokenVec myTokenVec; // Der Vector für die Tokens public: Scanner(const std::string& input); Token getNextToken(bool peek = false); private: void initTokenVec(); Token readNextToken(); void skipSpaces(); void readNextChar(); };Damit haben wir später die Möglichkeit abzufragen, welches Token folgt, ohne dabei in unserem Vector tatsächlich weiterzugehen. So können wir beim Parsen bequem entscheiden, ob es sich um eine Funktion oder eine Konstante handelt und das Problem beheben.
Natürlich müssen wir auch noch unsere Aufzählung von Tokens und so weiter ändern. Den Quellcode gebe ich dafür nicht an, aber wir brauchen ein neues Token für Bezeichner
TT_IDENTund für KommaTT_COMMA.Im Scanner sieht die Funktion
getNextTokendann nur noch so aus:Token Scanner::getNextToken(bool peek) { // Sind wir noch nicht am Ende der Liste? if (myVecPos < myTokenVec.size()) { if (!peek) { return myTokenVec[myVecPos++]; } return myTokenVec[myVecPos]; } return Token(TT_NIL); }Man sieht, wir verändern
myVecPosnicht, wennpeektrueist. Zur Füllung des Vectors schreiben wir uns noch eine Funktion, die im Konstruktor aufgerufen wird. Außerdem initialisieren wir natürlich die Variablen:Scanner::Scanner(const std::string& input) : myInput(input), myPos(0), myVecPos(0) // Initialisierungen { // Erstes Zeichen einlesen readNextChar(); // Alle Tokens einlesen und im Vector speichern initTokenVec(); } void Scanner::initTokenVec() { Token tok = readNextToken(); while (!tok.equal(TT_NIL)) { myTokenVec.push_back(tok); tok = readNextToken(); } }Die größte Veränderung beim Erkennen der Tokens ist hier zu sehen:
Token Scanner::readNextToken() { // ... switch (myCh) { // ... case ',': readNextChar(); return Token(TT_COMMA); case 'a': case 'b': case 'c': case 'd': case 'e': case 'f': case 'g': case 'h': case 'i': case 'j': case 'k': case 'l': case 'm': case 'n': case 'o': case 'p': case 'q': case 'r': case 's': case 't': case 'u': case 'v': case 'w': case 'x': case 'y': case 'z': case 'A': case 'B': case 'C': case 'D': case 'E': case 'F': case 'G': case 'H': case 'I': case 'J': case 'K': case 'L': case 'M': case 'N': case 'O': case 'P': case 'Q': case 'R': case 'S': case 'T': case 'U': case 'V': case 'W': case 'X': case 'Y': case 'Z': case '_': while (isalpha(myCh) || myCh == '_') { buf += myCh; readNextChar(); } return Token(TT_IDENT, 0, buf); case '0': case '1': case '2': case '3': case '4': case '5': case '6': case '7': case '8': case '9': // Einlesen, solange es eine Ziffer und kein Dezimalpunkt ist while (isdigit(myCh) && myCh != '.') { buf += myCh; readNextChar(); } // Dezimalzahl? if (myCh == '.') { buf += myCh; readNextChar(); if (!isdigit(myCh)) { std::cerr << "Error: die Dezimalzahl ist fehlerhaft" << std::endl; } else { while (isdigit(myCh)) { buf += myCh; readNextChar(); } } } // Der Einfachheit haben wir die Zahl zunächst in einen String eingelesen // Dieser wird nun in ein Double konvertiert return Token(TT_NUMBER, atof(buf.c_str())); // ... } return Token(TT_NIL); }Damit haben wir einen Scanner, der viel flexibler ist. Wir werden beim Parsen direkt einen Abstrakten Syntaxbaum nutzen, damit wir nicht später wieder alles ändern müssen. Daher hier die dazugekommenen Klassen:
class NodeIdent : public Node { private: std::string myName; public: NodeIdent(const std::string& name) : myName(name) { } const std::string& getName() const { return myName; } virtual double eval() const { if (myName == "pi") { return 3.14159265; } else if (myName == "c") { return 299792458; } else if (myName == "e") { return 2.71828183; } std::cerr << "Error: unbekannte Konstante '" << myName << "'" << std::endl; return 1; } };Wir überprüfen erst beim Aufruf von
eval, ob die Konstante existiert und welchen Wert sie hat. Im Fehlerfall geben wir eine Meldung aus und 1 zurück. Außerdem besitzt die Klasse eine FunktiongetName, mit der wir auf denstd::stringzugreifen können.Die Klasse
NodeFuncist etwas größer, aber die Erklärung folgt direkt nach dem Code:typedef std::vector<Node *> ArgVec; class NodeFunc : public Node { private: NodeIdent *myIdent; ArgVec myArgs; public: NodeFunc(NodeIdent *ident) : myIdent(ident) { } virtual ~NodeFunc() { for (ArgVec::iterator it = myArgs.begin(); it != myArgs.end(); ++it) { delete *it; } delete myIdent; } void pushArg(Node *node) { myArgs.push_back(node); } bool checkArgCount(unsigned int count) const { if (myArgs.size() != count) { std::cerr << "Error: " << count << " Parameter fuer '" << myIdent->getName() << "' erwartet" << std::endl; return false; } return true; } virtual double eval() const { if (myIdent->getName() == "sin") { if (checkArgCount(1)) { return sin(myArgs[0]->eval()); } } else if (myIdent->getName() == "cos") { if (checkArgCount(1)) { return cos(myArgs[0]->eval()); } } else if (myIdent->getName() == "tan") { if (checkArgCount(1)) { return tan(myArgs[0]->eval()); } } else if (myIdent->getName() == "sqrt") { if (checkArgCount(1)) { return sqrt(myArgs[0]->eval()); } } else if (myIdent->getName() == "pow") { if (checkArgCount(2)) { return pow(myArgs[0]->eval(), myArgs[1]->eval()); } } else { std::cerr << "Error: unbekannte Funktion '" << myIdent->getName() << "'" << std::endl; } return 1; } };Zunächst benötigen wir einen
std::vectordamit wir die Parameter der Funktion speichern können. Dieser Vector wird während des Parsings mit der FunktionpushArgbefüllt. Außerdem gibt es noch eine FunktioncheckArgCount, die überprüft, ob der Vector die angegebene Anzahl von Parametern enthält. Im Fehlerfall wird eine Fehlermeldung ausgegeben.Die Funktion
evalüberprüft dann einfach den Namen der Funktion und ob die entsprechende Anzahl von Parametern vorliegt. Ist das alles okay, wird die Funktion aufgerufen und das Ergebnis zurückgegeben. Ansonsten wird auch an dieser Stelle wieder 1 zurückgegeben und eine Fehlermeldung ausgegeben.Nun zum Parser: Durch die neue EBNF erkennen wir, dass wir zwei neue Funktionen benötigen. Und zwar die Funktion
funktionundbezeichner.Die Funktion
bezeichnerist wie die Funktionzahlsehr einfach:// Bezeichner = ( ('a' - 'Z') | '_' ) { ('a' - 'Z') | '_' } ; // Wir erhalten den gesamten Bezeichner vom Scanner: // Es ist hier also keine Zusammensetzung mehr notwendig! NodeIdent *Parser::bezeichner() { std::string ident = myTok.getStrValue(); accept(TT_IDENT); return new NodeIdent(ident); }Die Funktion
funktionenthält aber auch nicht viel neues:// Funktion = (Bezeichner) '(' [ (Start) { ',' (Start) } ] ')' ; NodeFunc *Parser::funktion() { NodeFunc *res = new NodeFunc(bezeichner()); accept(TT_LPAREN); if (!myTok.equal(TT_RPAREN)) { res->pushArg(start()); // Rekursion while (myTok.equal(TT_COMMA)) { accept(TT_COMMA); res->pushArg(start()); // Rekursion } } accept(TT_RPAREN); return res; }Man beachte, dass der Konstruktor von
NodeFuncdie Funktionbezeichneraufruft. Des Weiteren wird mit der FunktionpushArgder Vector gefüllt, falls Parameter vorhanden sind.Eine weitere Änderung erfolgt in der Funktion
klammer:// Klammer = ["+" | "-"] ((Funktion) | (Bezeichner) | (Zahl) | "(" (Start) ")") ; Node *Parser::klammer() { int sign = 1; // Für Vorzeichen (Standard: positives Vorzeichen) // Haben wir ein Vorzeichen? if (myTok.equal(TT_PLUS) || myTok.equal(TT_MINUS)) { if (myTok.equal(TT_MINUS)) { sign = -1; // Negatives Vorzeichen } getNextToken(); } // Haben wir eine Klammer? if (myTok.equal(TT_LPAREN)) { accept(TT_LPAREN); Node *res = start(); // Rekursion accept(TT_RPAREN); return new NodeMul(new NodeNumber(sign), res); } else if (myTok.equal(TT_IDENT)) { // Ist das folgende Token eine öffnende Klammer? if (myScanner.getNextToken(true).equal(TT_LPAREN)) { // Dann ist es eine Funktion return funktion(); } // Ansonsten eine Konstante return bezeichner(); } // Keine Klammer, also gehen wir von einer Zahl aus return new NodeMul(new NodeNumber(sign), zahl()); }Wenn keine öffnende Klammer gefunden wurde, wird überprüft, ob es sich um einen Bezeichner handelt. Ist das der Fall, dann müssen wir entscheiden, ob dieser Bezeichner eine Funktion beschreibt, also noch eine öffnende Klammer folgt oder ob es sich um eine Konstante handelt, also keine öffnende Klammer folgt.
Damit wir das überprüfen können, übergeben wir
getNextTokenden Parametertrue. So überprüfen wir das folgende Token ohne es tatsächlich zu lesen und die Positionsangabe im Scanner zu ändern. Das war unser Ziel, als wir den Scanner umgerüstet haben.Wenn wir also eine Klammer vorfinden, handelt es sich um eine Funktion. Ansonsten handelt es sich um einen Bezeichner. Wir geben das Ergebnis dieser Funktion natürlich auch mit
returnzurück.Damit haben wir eigentlich alles geschafft, was wir schaffen wollten. Man kann jetzt noch weiter machen und Fehlerabfragen einprogrammieren, ob z.B. eine Division durch 0 stattfindet. Dazu müsste man die
evalFunktion vonNodeDivverändern:virtual double eval() const { double right = myNodeRight->eval(); // Rechter Ausdruck ergibt nicht 0 if (right != 0) { return myNodeLeft->eval() / right; } std::cerr << "Error: Division durch 0" << std::endl; return 1; }Hier mal wieder ein paar Beispieleingaben und ihre Ausgaben:
Eingabe: pi
Ergebnis: 3.14159Eingabe: e
Ergebnis: 2.71828Eingabe: e + pi * pow(2, 2)
Ergebnis: 15.2847Eingabe: pow(pow(pow(2, 4), 2), pi)
Ergebnis: 3.67882e+007Eingabe: pow ( sin ( 4 - pi) * pow(3 + 1, 4 - 0), 1)
Ergebnis: 193.741Eingabe: sin() + pow()
Error: 1 Parameter fuer 'sin' erwartet
Error: 2 Parameter fuer 'pow' erwartet
Ergebnis: 2Eingabe: pow(1, 2)
Ergebnis: 1Eingabe: test * pi
Error: unbekannte Konstante 'test'
Ergebnis: 3.14159Eingabe: test() * pi
Error: unbekannte Funktion 'test'
Ergebnis: 3.14159Auch verschachtelte Funktionsaufrufe stellen kein Problem dar. Auch Leerzeichen und andere Leerräume bereiten noch immer keine Probleme.
10 Abschluss
Vielleicht hat ja schon jemand versucht, selbst einen solchen Matheparser zu entwickeln und hat einfach eine eigene Idee genutzt. War dieser auch so mächtig oder stieß man schnell an die Grenzen? Wenn man nach der hier vorgeschriebenen Idee vorgeht, dann kann man sehr robuste Programme schreiben. Dabei ist es egal, ob es sich um eine Syntax handelt, die die Mathematik beschreibt, oder um eine Syntax, die eine kleine Scriptsprache darstellt. Es ist sehr einfach, wenn man sich nur etwas Zeit nimmt und die EBNF versucht zu verstehen und anzuwenden.
Und wenn man sich den Code ansieht, dann stellt man fest, dass dieser nicht sehr umfangreich ist. Er würde sich sogar noch kürzen lassen, wenn man beim Abstrakten Syntaxbaum nicht für jede Rechenoperation einen eigenen Node erstellt sondern nur einen und stattdessen einen Parameter übergibt, welche Rechenart auszuführen ist (Im C# Programm wurde das so gelöst).
Auch könnte man für die Funktionen, wie
sin,cosoder die Konstanten je einen eigenen Node erzeugen und damit die If-Abfragen vermeiden. Oder man programmiert alles so, dass es ganz einfach erweiterbar ist. Doch die zugrundeliegende Idee bleibt natürlich gleich.Wie anfangs erwähnt, würde ich diesen Artikel gerne fortsetzen und im nächsten Teil tatsächlich auf die Entwicklung einer kleinen Scriptsprache eingehen, falls dazu das Interesse besteht. Dabei sollen die vorgestellten Ideen von Scanner, Parser, Abstraktem Syntaxbaum weiter ausgebaut und praktisch eingesetzt werden.
11 Downloads
-
Ich finde NodeFunc unguenstig. Warum nicht genau wie Add fuer jede Funktion eine extra Klasse wie:
class Cos : public Node { public: Cos(Node* right); virtual double eval(); };Auch wuerde ich der eval-Methode (oder dem Konstruktor) einen Kontext mitgeben, in der Variablen und Konstanten definiert sind.
-
Hallo Dummie,
da Compilerbau mein Spezialgebiet an der Uni war, habe ich mich auch privat damit weiter beschäftigt.
Zuerst in C++: http://www.bitel.net/dghm1164/downloads/FctParser-Sources.zip
(für den Borland C++ Builder) - dieser ist auch in einigen Beiträgen hier im Forum schon verlinkt.Und ähnlich wie du habe ich dann einen Artikel verfasst (jedoch für C#): http://www.mycsharp.de/wbb2/thread.php?threadid=71995
Mein MathParser ist jedoch so allgemein gehalten, daß man die Operatoren, Funktionen und Konstanten jeweils selber der Basisklasse übergeben kann (auch die interne Optimierung als Abstract Syntax Tree ist implementiert!), d.h. es gibt eine allgemeine NodeFunc-Klasse (welche knivil ja angemeckert hat -).
Ich finde es schön, daß du dir die Mühe für diesen Artikel gemacht hast. Und ich wäre sehr an einer Fortsetzung interessiert (ich selber hatte vor ca. 13 Jahren mal eine eigene Scriptsprache in Delphi 2 (!) implementiert)...
-
Hallo Dummie
Ich finde den Artikel sehr interessant und gut beschrieben. Das ganze schaut sehr ausbaufähig aus und auch ich wäre sehr interessiert an einer Fortsetzung.
Wollt auch schon mal mit einer Scriptsprache anfangen aber ich schaff es immer nicht Projekte für die ich keinen direkten Sinn (Anwendung) finde zu Ende zu bringen :-). Deswegen großen Respekt an dir das du dir die ganze Mühe gemacht hast und auch noch einen Artikel dafür geschrieben hast.
Mfg Marco
-
Hallo,
danke für die positiven Kommentare

knivil schrieb:
Ich finde NodeFunc unguenstig. Warum nicht genau wie Add fuer jede Funktion eine extra Klasse wie:
class Cos : public Node { public: Cos(Node* right); virtual double eval(); };Auch wuerde ich der eval-Methode (oder dem Konstruktor) einen Kontext mitgeben, in der Variablen und Konstanten definiert sind.
In dem Fall müsste man beim Parsing entscheiden, welcher Node angelegt werden muss. Das lässt sich sicherlich gut über ein Array o. ä. erledigen - so ließen sich auch viel einfacher neue Funktion hinzufügen. Für diesen Artikel fand ich das Vorgehen über NodeFunc aber als verständlicher.

Th69 schrieb:
Mein MathParser ist jedoch so allgemein gehalten, daß man die Operatoren, Funktionen und Konstanten jeweils selber der Basisklasse übergeben kann (auch die interne Optimierung als Abstract Syntax Tree ist implementiert!), d.h. es gibt eine allgemeine NodeFunc-Klasse (welche knivil ja angemeckert hat -).
Dein Matheparser ist auch wirklich sehr interessant, insbesondere da er so allgemein gehalten ist. Ich hatte ja auch im Artikel beschrieben, dass man das machen kann, damit haben wir ja nun auch dafür ein schönes Beispiel.

Marc-O schrieb:
Wollt auch schon mal mit einer Scriptsprache anfangen aber ich schaff es immer nicht Projekte für die ich keinen direkten Sinn (Anwendung) finde zu Ende zu bringen :-). Deswegen großen Respekt an dir das du dir die ganze Mühe gemacht hast und auch noch einen Artikel dafür geschrieben hast.
Ja, so eine Sprache ist auch schon ein etwas größerer Akt. Selbst eine sehr kleine Scriptsprache kann schon sehr viel Arbeit bedeuten und man stellt erst beim Programmieren fest, was moderne Sprachen tatsächlich alles für einen leisten. Das was man schon lange als selbstverständlich empfunden hat, vermisst man plötzlich bei der eigenen.

-
Hi,
ich schreibe keine parser mehr selbst. boost::spirit kann das viel besser.
Chris
-
Sehr schöner Artikel und sehr interessant!
-
chrmhoffmann schrieb:
Hi,
ich schreibe keine parser mehr selbst. boost::spirit kann das viel besser.
Chris
Habs mir mal angeschaut und muss sagen ist sehr interressant, wobei ich einiges aus dem Artikel direkt mitnehmen konnte für diese Bibliothek, und wenn es auch nur das EBNF ist

Aber ansonst werd ich mir die mal genauer anschauen und versuchen nen kleinen XML-Parser damit zu bauen.
Mfg marco
-
flex + bison

-
Das ist wohl eines der Besten C Tutorials, das ich je gesehen hab, Respekt!
 Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen
Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen 
Nochmal rechten Dank!
Mfg iJake1111
-
Toller Artikel, hat mir sehr geholfen!
-
iJake1111 schrieb:
Das ist wohl eines der Besten C Tutorials, das ich je gesehen hab, Respekt!
 Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen
Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen 
Nochmal rechten Dank!
Mfg iJake1111Leider ist es C++
-
leiderC++ schrieb:
iJake1111 schrieb:
Das ist wohl eines der Besten C Tutorials, das ich je gesehen hab, Respekt!
 Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen
Seit diesem Tut, sehe ich Parser schon mit ganz anderen Augen 
Nochmal rechten Dank!
Mfg iJake1111Leider ist es C++
Ich habe die einfache Version in C portiert. Steht also ab jetzt auch zum Download bereit. Vielleicht interessiert sich ja jemand dafür.

-
Als Stichwort: Parser Combinator
-
OK. Ich habe mir das Tutorial zu Gemüte geführt und den Quelltext erstmal gedownloadet. Wenn ich diesen kompiliere, geht noch alles glatt. Wenn das Programm dann allerdings startet, kann ich auch ohne Probleme meinen String eingeben, nachdem ich 'Enter' gedrückt habe, kommt aber immer folgende Meldung: "Debug Assertion Failed! ....". Wenn ich dann auf ignorieren klicke, steht das Ergebnis auch da. Wie kriege ich also die Fehlermeldung weg?
Schonmal danke im Voraus.
-
Ich hab mir jetzt den Quellcode nicht angesehen, aber mein erster Anhaltspunkt wäre, dass man nach einem "assert" Ausschau hält und herausfindet, warum das fehlschlägt.
-
Hey,
probier mal in der Datei Scanner.cpp die Funktion
Scanner::readNextChar()zu suchen und ersetz in dieser die Zeileif (myPos > myInput.length())durch diese Zeile (es kommt ein = hinzu):
if (myPos >= myInput.length())Warum aber der Fehler erst jetzt auftritt ist mir nicht klar. Vermutlich hat es was mit der neu herausgekommenen Visual Studio Version oder 32 Bit bzw. 64 Bit Systemen zu tun. Mir wäre der Fehler (der unabhängig von der Eingabe immer auftritt) sonst definitiv aufgefallen.
Vielen Dank für die Rückmeldung

Edit:
Falls jemand parallel zu neuren Versionen noch die alte Version installiert hat, wäre es wirklich sehr nett, wenn jemand überprüfen könnte, ob der Fehler dort auch auftritt und ob length() in den Versionen vielleicht unterschiedliche Werte zurückliefert oder ob in der Bibliothek einfach ein Assert dazugekommen ist.
-
* AUSGRABE*
Eine frage kann man den download auch so bekommen das man das aus Linux ohne VS öffnen kann?

Einfach .txt reicht mir.
-
Enno schrieb:
* AUSGRABE*
Eine frage kann man den download auch so bekommen das man das aus Linux ohne VS öffnen kann?

Einfach .txt reicht mir.
Der Quellcode in C bzw. C++ ist plattformunabhängig und in den Downloads natürlich ebenso enthalten.
Also alles entpacken und in das entsprechende Verzeichnis gehen, wo die .h und .cpp Dateien liegen.
Dann für die C++ Variante einfach: g++ -o Prog *.h *.cpp
Und zum Starten: ./Prog
Ansonsten bietet es sich an, dass du den Artikel einfach Schritt für Schritt bearbeitest. Es ist immer sinvoller, wenn man auch die ganzen Hintergründe versteht.

-
Dummie schrieb:
Enno schrieb:
* AUSGRABE*
Eine frage kann man den download auch so bekommen das man das aus Linux ohne VS öffnen kann?

Einfach .txt reicht mir.
Der Quellcode in C bzw. C++ ist plattformunabhängig und in den Downloads natürlich ebenso enthalten.
Also alles entpacken und in das entsprechende Verzeichnis gehen, wo die .h und .cpp Dateien liegen.
Dann für die C++ Variante einfach: g++ -o Prog *.h *.cpp
Und zum Starten: ./Prog
Ansonsten bietet es sich an, dass du den Artikel einfach Schritt für Schritt bearbeitest. Es ist immer sinvoller, wenn man auch die ganzen Hintergründe versteht.

Danke für deine antwort werd das gleich ausprobieren. Ich arbeite das grade durch und wollte nur mal nachgucken wo du die
enum TokenTypehingepackt hast.

EDIT: Da kommt bei mir gleich die frage auf ob man das nicht alles in 3 Datei machen kann? muss ich das alles so auslagern?