[A]Algorithmen/Datenstrukturen: Einfach-/Doppeltverkettete Listen
-
Inhaltsverzeichnis
- Einleitung
- Struktur von Listen
- Einfachverkette Listen
- Doppeltverkette Listen
- Fazit
1 Einleitung
Um effiziente Programme erstellen zu können, braucht man immer wieder verschiedene Datenstrukturen auf denen dann verschiedene Algorithmen laufen müssen. In dieser Artikelreihe werden wir uns mit diversen Datenstrukturen und auch einigen Algorithmen befassen.Speziell in diesem Artikel werde ich einen kleinen Einblick in einfach- bzw. doppeltverkettete Listen geben. In den einzelnen Kapiteln wird durch Beispiele gezeigt, wo und wie Listen verwendet werden können.
2 Struktur von Listen.
Um Listen darstellen zu können benötigt man zu Beginn erst einmal das Aussehen eines Listenelementes. Das könnte beispielsweise so aussehen./* C Variante */ struct Listenelement { /* Zu verwaltende Daten im Listenelement */ /* ... */ /* Zeiger auf das nächste Element */ struct Listenelement* next; /* Bei einer Doppeltverkettung benötigen wir auch noch */ /* einen Zeiger auf das vorherige Element */ struct Listenelement* prev; }; /* cpp Variante */ class Listenelement { public: Listenelement() { } Listenelement(/*übergabe von zu speichernden Daten*/) { /*Daten initialisieren*/ } private: // Die Listenzeiger Listenelement* next; Listenelement* prev; };Neben der Struktur für das Listenelement brauchen wir noch das Aussehen für die Liste selbst. Normalerweise würde uns ein Zeiger auf ein Listenelement genügen, allerdings ist es geschickter sich eine eigene Struktur bzw. Klasse für die Liste zu definieren, da listenspezifische Dinge wie etwa die Anzahl der Listenelemente in dieser Struktur/Klasse gespeichert werden können.
Die Liste selbst könnte dann wie folgt aussehen.
/* C Variante */ struct Liste { /* Listenbeginn */ struct Listenelement* start; /* Anzahl der Elemente */ int Elementanzahl; }; /* cpp Variante */ class Liste { public: Liste { } Liste(/*übergabe von zu speichernden Daten*/) { /*Daten initialisieren*/ } private: /* Listenbeginn */ Listenelement* start; /* Anzahl der Elemente */ int Elementanzahl; };
-
Salute,
ich muss noch mal stören. Ich sehe gerade, dass du sowohl die C als auch die C++ Variante zeigst... hat das nen bestimmten Grund? Mir wäre es, wenn du nur eine zeigst. Entweder C oder C++. Ich würde C vorschlagen, da es u.a. einfacher is, den C Code auf C++ umzusatteln, als von C++ auf C runter zu müssen. Du kannst aber auch gerne C++ nehmen. Oder anders gesagt: Nimm die Sprache, in der du fitter bist

Wir könnten ja die Parallelimplementierung als Download zur Verfügung stellen, das wäre imo ein guter Mittelweg. Oder?
Grüße
GPC
-
OK,
ich wollt es halt für beide machen. Aber dann mach ich es in C und die C++ Variante kommt dann als Download mit rein.
Grüsse
Tobi
-
Gut, aber wie gesagt, wenn du lieber die C++ Variante zeigen und die C als Download anbieten willst, kein Problem.
-
Inhaltsverzeichnis
- Einleitung
- Struktur von Listen
- Einfachverkette Listen
- Doppeltverkette Listen
- Fazit
1 Einleitung
Um effiziente Programme erstellen zu können, braucht man immer wieder verschiedene Datenstrukturen auf denen dann verschiedene Algorithmen laufen müssen. In dieser Artikelreihe werden wir uns mit diversen Datenstrukturen und auch einigen Algorithmen befassen.Speziell in diesem Artikel werde ich einen kleinen Einblick in einfach- bzw. doppeltverkettete Listen geben. In den einzelnen Kapiteln wird durch Beispiele gezeigt, wo und wie Listen verwendet werden können.
2 Struktur von Listen.
Um Listen darstellen zu können benötigt man zu Beginn erst einmal das Aussehen eines Listenelementes. Das könnte beispielsweise so aussehen./* C Variante */ struct Listenelement { /* Zu verwaltende Daten im Listenelement */ /* ... */ /* Zeiger auf das nächste Element */ struct Listenelement* next; /* Bei einer Doppeltverkettung benötigen wir auch noch */ /* einen Zeiger auf das vorherige Element */ struct Listenelement* prev; };Neben der Struktur für das Listenelement brauchen wir noch das Aussehen für die Liste selbst. Normalerweise würde uns ein Zeiger auf ein Listenelement genügen, allerdings ist es geschickter sich eine eigene Struktur bzw. Klasse für die Liste zu definieren, da listenspezifische Dinge wie etwa die Anzahl der Listenelemente in dieser Struktur/Klasse gespeichert werden können.
Die Liste selbst könnte dann wie folgt aussehen.
/* C Variante */ struct Liste { /* Listenbeginn */ struct Listenelement* start; /* Anzahl der Elemente */ int Elementanzahl; //... };Die Basisoperationen bei verketteten Listen sind "Element einfügen" und "Element löschen". Implementierungen dieser und weiterer Operaptionen werden in den nächsten beiden Kapiteln gezeigt.
3 Einfachverkettete Listen
-
Hallo!
Ich habe das hier mal kurz überflogen und habe ein paar Empfehlungen dazu. Das Netz ist voll von Tutorials mit doppelt verketteten Listen.
Leider wird bei 99% dieser Listen eine etwas ungeschickte Implementierung verwendet, indem das Ende der Liste durch einen Null-Pointer markiert wird.Ich kann hier noch nicht erkennen, was es mal werden soll, würde aber, auch um den Artikel von anderen ein bißchen abzuheben auf jeden Fall eine andere Variante ohne Null als Ende vorschlagen. Das ist afaik auch der Weg, den die meisten STL-Implementierungen gehen. Die Einführung eines Dummy-Knotens macht die Suche performanter, erleichtert die Implementierung von Iteratoren und macht den Code einfacher. Man bezahlt dafür nur die Kosten für den Speicher eines einzelnen ListNodes.
MfG Jester
edit: da ich auf dem Forumtreffen sowas in der Art eh in nem Vortrag erzählen werde, kann ich Dir gerne ein paar Folien dazu schicken (auch wenn die alles andere als ausführlich sind).
-
Hallo Jester,
erstmal danke für die Tipps.
Ich hatte nicht vor, das Ende der Liste mit einem Nullpointer zu makieren. Auch die Idee mit dem Dummy Knoten ist mir schon gekommen. Mal sehen wie ich das realisiere. Muss wohl meine alten Vorlesungsunterlagen nochmal durchkauen ;).
Für die Folien wäre ich dir dankbar.
Grüsse
Tobi
-
Inhaltsverzeichnis
- Einleitung
- Struktur von Listen
- Einfachverkette Listen
- Doppeltverkette Listen
- Fazit
1 Einleitung
Um effiziente Programme erstellen zu können, braucht man immer wieder verschiedene Datenstrukturen auf denen dann verschiedene Algorithmen laufen müssen. In dieser Artikelreihe werden wir uns mit diversen Datenstrukturen und auch einigen Algorithmen befassen.Speziell in diesem Artikel werde ich einen kleinen Einblick in einfach- bzw. doppeltverkettete Listen geben. In den einzelnen Kapiteln wird durch Beispiele gezeigt, wo und wie Listen verwendet werden können.
2 Struktur von Listen.
Um Listen darstellen zu können benötigt man zu Beginn erst einmal das Aussehen eines Listenelementes. Das könnte beispielsweise so aussehen./* C Variante */ struct Listenelement { /* Zu verwaltende Daten im Listenelement */ /* ... */ /* Zeiger auf das nächste Element */ struct Listenelement* next; /* Bei einer Doppeltverkettung benötigen wir auch noch */ /* einen Zeiger auf das vorherige Element */ struct Listenelement* prev; };Neben der Struktur für das Listenelement brauchen wir noch das Aussehen für die Liste selbst. Normalerweise würde uns ein Zeiger auf ein Listenelement genügen, allerdings ist es geschickter sich eine eigene Struktur bzw. Klasse für die Liste zu definieren, da listenspezifische Dinge wie etwa die Anzahl der Listenelemente in dieser Struktur/Klasse gespeichert werden können.
Die Liste selbst könnte dann wie folgt aussehen.
/* C Variante */ struct Liste { /* Listenbeginn */ struct Listenelement* start; /* Anzahl der Elemente */ int Elementanzahl; //... };Die Basisoperationen bei verketteten Listen sind "Element einfügen" und "Element löschen". Implementierungen dieser und weiterer Operaptionen werden in den nächsten beiden Kapiteln gezeigt.
3 Einfachverkettete Listen
Bei einfachverketteten Listen gibt es "nur" eine Vorwärtsverkettung. Das bedeutet, dass jeder Knoten nur seinen Nachfolger, nicht aber seinen Vorgänger kennt.[bild]
...
[/bild]Im folgenden bauen wir uns eine Liste mit Beispieldaten auf. Die aneinanderzuhängenden Informationen sind hierbei der Einfachheit halber Integerwerte.
3.1 Die klassische Implementierung
Zunächst das Listenelement (die Node)typedef struct ListNode { int data; /* hier steht ein beliebiger Datentyp (auch Stukturen) */ ListNode* next; };Dann benötigen wir unsere Listenstruktur
typedef struct List { ListNode* begin; int ElementCounter; List() { begin = NULL; ElementCounter = 0; } };Als nächster Schritt ist eine Ein- bzw Anfügen Operation zu realisieren.
// unsortiertes Einfügen in die Liste int InsertIntoList(List* list, int data) { //keine Liste? Schlecht! return if(!list) return 1; //Liste leer? if(list->begin == NULL) { // platz reservieren list->begin = (ListNode*)malloc(sizeof(ListNode)); // Malloc schlägt fehl if(!(list->begin)) return 1; // Daten schreiben list->begin->data = data; list->begin->next = NULL; } //ansonsten else { // Laufknoten ListNode* node; node = list->begin; // ans Ende hangeln while(node->next != NULL) node = node->next; // Speicher reservieren node->next = (ListNode*)malloc(sizeof(ListNode)); if(!node) return 1; // Daten schreiben node->next->data = data; node->next->next = NULL; } ++(list->ElementCounter); return 0; }[Anmerkung: Den Code verbessere ich noch war jetzt nur mal aus dem Kopf hingefrickelt]
Als nächstes braucht es natürlich noch eine Löschoperation
...
-
Tobias Gerg schrieb:
int InsertIntoList(List* list, int data) { //keine Liste? Schlecht! return if(!list) return 1; //Liste leer? if(list->begin == NULL) { // platz reservieren list->begin = (ListNode*)malloc(sizeof(ListNode)); // Malloc schlägt fehl if(!(list->begin)) return 1; // Daten schreiben list->begin->data = data; list->begin->next = NULL; } //ansonsten else { // Laufknoten ListNode* node; node = list->begin; // ans Ende hangeln while(node->next != NULL) node = node->next; // Speicher reservieren node->next = (ListNode*)malloc(sizeof(ListNode)); if(!node) return 1; // Daten schreiben node->next->data = data; node->next->next = NULL; } ++(list->ElementCounter); return 0; }naja, man versteht irgendwie, wie du drauf kommst.
den ElementCounter würde ich wegwerfen und auch void returnen.das ans-ende-hangeln verstehe ich nicht. füge doch am anfang ein.
und dann hilft von der naiven implemetierung zum ferrari der listen volkards bewähtes 5-punkte-tuning für verhettete listen.
schritt1:
oder du willst unbedingt ne lifo und keine fifo, dann merk die anfangs- und endezeiger. problem: zu viel if unf alles schwer zuz lesen und zu schreiben.schritt2:
mach nen ring draus. ein bisschen if geht schon weg.schriit3:
und merk die den letzten knoten statt beiden. member gespart und updatearbeit.schritt4:
leg am anfang nen dummyknoten an, und merk dir den. sorge damit dafür, daß die liste nie leer ist. kein if mehr!

schritt5:
mach noch die indirektion weg, indem der dummyknoten selbst dein member ist und nicht ein zeiger drauf.die ganzen schritte würde ich am insert vormachen. jede zwischenstufe ausprogrammiert. die anderen methoden kann man dann direkt an den ferrari löten.
außerdem ist die verwandlung der nativen implementierung in den ferrari bei der doppelt verketteten liste besser und am ende steht auch eine vollständige klasse da, an der nichts fehlt oder ungeschickt ist.
bei der einfach verketteten liste haste eine remove-methode der zeitkomplexität o(n). die wirste fein los mit nem iterator, der aufs vorgängerelement zeigt (nebst wunderbarkeit, daß remove(it);++it; geht und der iterator nicht zerstört wurde). da wäre es vielleicht nett, die dopplet verkettete vor der einfach verketteten zu machen.
-
volkard schrieb:
(nebst wunderbarkeit, daß remove(it);++it; geht und der iterator nicht zerstört wurde). da wäre es vielleicht nett, die dopplet verkettete vor der einfach verketteten zu machen.
Aber das löschen könnte andere Iteratoren invalidieren, obwohl ihre Knoten nicht gelöscht werden. Klingt unschön.
Vielleicht kann man in singly linked-lists einfach kein schönes delete anbieten.
-
Jupp, ich weiß schon was du meinst, der Code war auch nur ein gefrickel von mir... Ich bieg dass noch gerade...
Trotzdem danke für die Tipps. Werd mich dran halten...
Grüsse
Tobi
-
Inhaltsverzeichnis
- Einleitung
- Struktur von Listen
- Einfachverkette Listen
- Doppeltverkette Listen
- Fazit
1 Einleitung
Um effiziente Programme erstellen zu können, braucht man immer wieder verschiedene Datenstrukturen auf denen dann verschiedene Algorithmen laufen müssen. In dieser Artikelreihe werden wir uns mit diversen Datenstrukturen und auch einigen Algorithmen befassen.Speziell in diesem Artikel werde ich einen kleinen Einblick in einfach- bzw. doppeltverkettete Listen geben. In den einzelnen Kapiteln wird durch Beispiele gezeigt, wo und wie Listen verwendet werden können.
2 Struktur von Listen.
Um Listen darstellen zu können benötigt man zu Beginn erst einmal das Aussehen eines Listenelementes. Das könnte beispielsweise so aussehen./* C Variante */ struct Listenelement { /* Zu verwaltende Daten im Listenelement */ /* ... */ /* Zeiger auf das nächste Element */ struct Listenelement* next; /* Bei einer Doppeltverkettung benötigen wir auch noch */ /* einen Zeiger auf das vorherige Element */ struct Listenelement* prev; };Neben der Struktur für das Listenelement brauchen wir noch das Aussehen für die Liste selbst. Normalerweise würde uns ein Zeiger auf ein Listenelement genügen, allerdings ist es geschickter sich eine eigene Struktur bzw. Klasse für die Liste zu definieren, da listenspezifische Dinge wie etwa die Anzahl der Listenelemente in dieser Struktur/Klasse gespeichert werden können.
Die Liste selbst könnte dann wie folgt aussehen.
/* C Variante */ struct Liste { /* Listenbeginn */ struct Listenelement* start; /* Anzahl der Elemente */ int Elementanzahl; //... };Die Basisoperationen bei verketteten Listen sind "Element einfügen" und "Element löschen". Implementierungen dieser und weiterer Operaptionen werden in den nächsten beiden Kapiteln gezeigt.
3 Einfachverkettete Listen
Bei einfachverketteten Listen gibt es "nur" eine Vorwärtsverkettung. Das bedeutet, dass jeder Knoten nur seinen Nachfolger, nicht aber seinen Vorgänger kennt.[bild]
...
[/bild]Im folgenden bauen wir uns eine Liste mit Beispieldaten auf. Die aneinanderzuhängenden Informationen sind hierbei der Einfachheit halber Integerwerte.
3.1 Die klassische Implementierung
Zunächst das Listenelement (die Node)typedef struct ListNode { int data; /* hier steht ein beliebiger Datentyp (auch Stukturen) */ ListNode* next; };Dann benötigen wir unsere Listenstruktur
typedef struct List { ListNode* begin; int ElementCounter; List() { begin = NULL; ElementCounter = 0; } };Als nächster Schritt ist eine Ein- bzw Anfügen Operation zu realisieren.
// unsortiertes Einfügen in die Liste int InsertIntoList(List* list, int data) { //keine Liste? Schlecht! return if(!list) return 1; //Liste leer? if(list->begin == NULL) { // platz reservieren list->begin = (ListNode*)malloc(sizeof(ListNode)); // Malloc schlägt fehl if(!(list->begin)) return 1; // Daten schreiben list->begin->data = data; list->begin->next = NULL; } //ansonsten else { // Laufknoten ListNode* node; node = list->begin; // ans Ende hangeln while(node->next != NULL) node = node->next; // Speicher reservieren node->next = (ListNode*)malloc(sizeof(ListNode)); if(!node) return 1; // Daten schreiben node->next->data = data; node->next->next = NULL; } ++(list->ElementCounter); return 0; }Nun ja, wie man sieht ist das ziemlich umständlich. Darum führen wir ein Dummyelement ein, an das wir die Elemente anhängen.
[bild]
...
[/bild]Der Code dazu sieht wie folgt aus.
typedef struct List { ListNode* end; int ElementCounter; List() { end = (ListNode*)malloc(sizeof(ListNode)); if(!end) return; end->next = end; end->data = 0xFFFF; // ein Wert der in der normalen Liste // NICHT angenommen wird. ElementCounter = 0; } };int insert(List* l, int data) { if(!l) return 1; //Speicher für Element reservieren ListNode* inserter = (node*)malloc(sizeof(node)); if(!inserter) return 1; //Element einfügen (vor Enddummy) inserter->next = l->end->next; inserter->data = data; l->end->next = inserter; ++(l->ElementCounter); return 0; }Der Dummy end, der für den begin Knoten ins Spiel gekommen ist, erleichert uns die Arbeit ungemein. Die Überprüfung ob die Liste leer ist entfällt komplett, da wir zu Beginn ein Dummyelement besitzen.
Und das Einfügen geht somit auch leicht von der Hand, da wir immer am Beginn der Liste das neue Element einfügen. Damit haben wir eine LIFO Liste realisiert.
Es gibt unzählige weitere Methoden Einfügeoperationen zu realisieren. Man könnte beispielsweise einen FIFO realisieren, indem man den Next Zeiger des Dummy immer auf das Element vor dem Dummy zeigen lässt.
Als nächstes braucht es natürlich noch eine Löschoperation. Diese ist nicht so einfach zu realisieren wie es vielleicht zu begin aussehen mag, da die Verkettungsinformation nicht verloren gehen darf.
//liste löschen int deleteList(List* l) { if(!l) return 1; //zwei laufzeiger ListNode* run1, *run2; run1 = run2 = l->end->next; //solange elemente (einschließlich enddummy) //vorhanden. löschen while(run2) { //run2 aufs nächste Element setzen run2 = run1->next; //vorheriges Element löschen free(run1); //run1 nachrücken run1 = run2; //vom Ende entkoppeln l->end->next = NULL; } l->end = NULL; return 0; }Bei diesem Code läuft man immer um ein Element voraus, und löscht dann den vorhergehenden. Mit l->end->next = NULL entkoppelt man den Endzeiger vom ersten Element und bricht so den Ring auf, damit man nicht in eine Endlosschleife mit Speicherverletzungen kommt.
Als nächstes betrachen wir noch zwei andere Operationen auf die Liste. Das Finden und Löschen von einzelnen Elementen.
Das Finden:
int findElement(List* l, int data) { if(!l) return 1; int count = 0; node* run = l->end->next; //durch die Liste laufen while(run != l->end) { //gefunden? if(run->data == data) return count; //weitersuchen run = run->next; count++; } return -1; }Man läuft einfach durch die Liste und vergleicht die Elemente. Wird das Element gefunden liefern wir seine Position zurück ansonsten -1.
Das Löschen eines einzelnen Elements:
//ein Element löschen bool deleteElement(List* l, int data) { node* run, *pdelete; run = l->end; do { //gefunden if(run->next->data == data) { //Zeiger umhängen und Element merken pdelete = run->next; run->next = run->next->next; //Element löschen free(pdelete); --(l->ElementCounter); return true; } //weitersuchen run = run->next; } while(run != l->end); return false; }Auch beim Löschen laufen wir durch die Elemente der Liste bis wir das zu Löschende gefunden haben. Wir merken uns das Element und hängen die Zeiger entsprechend um. Danach wird das Element gelöscht.
Auch hier gibt es wieder unzählige Strategien um Zeit und Kosten zu sparen. Zum Beispiel wäre es möglich, die Elemente die zu Löschen sind in einen Pool zu hängen und sich beim Einfügen aus diesem Pool zu bedienen. Das spart etwa die Speicherallokation beim Einfügen neuer Elemente.
Mehr zu diesem Thema gibt es in den Literaturhinweisen.

4 Doppeltverkettete Listen
...
-
Morgen,
auch hier die Frage, wie's zum nächsten Termin aussieht? Bitte um realistische Werte

Grüße
GPC
-
0 Inhaltsverzeichnis
- Die Liste als Datenstruktur
- Einfach verkettete Liste
- Doppelt verkettete Liste
- Typlisten (Listen zur Compilezeit)
- Verwendundsbeispiele
...
-
Inhaltsverzeichnis
- Die einfach verkettete Liste
- Die doppelt verkettete Liste
- Typlisten
- Anwendungsgebiete
1 Die einfachverkettete Liste
Eine Liste besteht zunächst einmal aus Knoten die miteinander verknüpft werden. Das könnte so aussehen.
template <typename data_t> class singleLinkedNode { public: singleLinkedNode() : next_(0) {} singleLinkedNode(data_t data) : next_(0), data_(data) {} singleLinkedNode<data_t>* next_; data_t data_; };Wie man hier sieht, gibt es nur einen Next Zeiger. Das bedeutet dass der Knoten seinen Nachfolger, nicht aber seinen Vorgänger kennt.
Die Liste die diese Knotenstruktur verwaltet definiert einen head Zeiger sowie einen current/end Zeiger. Diese beiden Zeiger erlauben ein schnelles Einfügen am Ende bzw. am Anfang der Liste.
template <typename data_t> class singleLinkedList { public: // Constructor for the list singleLinkedList() { head_ = 0; current_ = 0; } private: singleLinkedNode<data_t>* head_; singleLinkedNode<data_t>* current_; };Der Konstruktor der Liste setzt die beiden Element auf Null.
Als nächstes benötigen wir eine insert Funktion. Die Funktion fügt Elemente am Ende der Liste ein.
// Construtor // ... // ... // insert something into list void insert(data_t data) { if(head_== 0) { // list is empty // insert first element and point head and current to the new element head_ = new singleLinkedNode<data_t>(data); current_ = head_; } else { // something is in the list // insert a element at the end singleLinkedNode<data_t>* temp = new singleLinkedNode<data_t>(data); current_->next_ = temp; current_ = temp; /*** if you want to insert the element at the beginning do it like this head = temp; temp->next = data; ***/ } } // private SachenDie Funktion prüft ab ob die Liste leer ist. Wenn dass der Fall ist, wird ein neues Element in die Liste eingefügt, head_ wird auf das neue Element gebogen und current_ zeigt ebenfalls auf das Element.
Ist die Liste nicht leer wird ein neues Objekt erzeugt und current_->next_ wird auf das neue Element temp gebogen (Die Verknüpfung). Danach wird der eigentliche current_ Zeiger auf das neue Element gebogen.
Soweit so gut. Da man hier aber mit new operiert, muss irgendwann einmal der Speicher aufgeräumt werden. Das erledigen wir im Destruktor der so aussehen könnte.
~singleLinkedList() { singleLinkedNode<data_t>* run, *del; run = head_; while(run != NULL) { del = run; run = run->next_; delete del; } }Der Destruktor läuft durch die Liste und löscht der Reihe nach ihre Elemente.
Als nächstes wäre es interessant zu sehen ob die ganze Konstruktion überhaupt funktioniert. Dazu schreiben wir eine ListOutput Funktion.
// Konstruktor // insert // Destructor // .. // .. void ListOutput() { singleLinkedNode<data_t>* run = head_; while(run != NULL) { std::cout << run->data_ << std::endl; run = run->next_; } } // private Deklarationen // ...Im Prinzip funktioniert die Ausgabefunktion wie der Destruktor. Wir laufen wieder durch die Liste. Nur diesmal geben wir die in der Liste vorhanden Daten aus.
Ein mögliches Testprogramm könnte so aussehen.
int main(void) { singleLinkedList<int> list; list.insert(1); list.insert(2); list.ListOutput(); std::cin.get(); return 0; }Natürlich braucht eine Liste noch mehr Funktionalität. Dazu gehören unter anderem Funktionen wie delete, deleteAt, find und getAt die wir als nächstes Implementieren.
....
FRAGE AN ALLE
Soll ich nen rekursiven Aufbau von Listen auch machen? So was in der Art wie
hier meine ich.template <typename data_> class MyList { public: MyList(data_ data, MyList<data_>* Tail = NULL) : head(data), tail(Tail){} MyList<data_>& insert(MyList<data_>& Tail) { tail = &Tail; return *this; } void Output() { MyList<data_>* run = this; while(run != NULL) { std::cout << run->head << std::endl; run = run->tail; } } data_ head; MyList* tail; }; int main() { MyList<int> a(0); MyList<int> b(1); MyList<int> c(2); a.insert(b.insert(c)); //a.Output(); MyList<int> d(3, &a); d.Output(); std::cin.get(); return 0; }Typlisten werden ja "ähnlich" aufgebaut...
FRAGE ENDE
-
Soll ich nen rekursiven Aufbau von Listen auch machen?
Ich fände es gut wenn es drin wäre, aber letzten endlich muss du das selbst wissen.
-
Letztlich glaube ich, dass man es fast reinmachen muss. Vorallem wenn ich dann noch Typlisten mache.
Ich denke dass ich es einbaue...
Gruß
Tobi
-
Inhaltsverzeichnis
- Die einfach verkettete Liste
- Die doppelt verkettete Liste
- Typlisten
- Anwendungsgebiete
1 Die einfachverkettete Liste
Eine Liste besteht zunächst einmal aus Knoten die miteinander verknüpft werden. Eine Knotendefinition könnte so aussehen.
template <typename data_t> class singleLinkedNode { public: singleLinkedNode() : next_(0) {} singleLinkedNode(data_t data) : next_(0), data_(data) {} singleLinkedNode<data_t>* next_; data_t data_; };Wie man hier sieht, gibt es nur einen Next Zeiger. Das bedeutet dass der Knoten seinen Nachfolger, nicht aber seinen Vorgänger kennt.

Die Liste die diese Knotenstruktur verwaltet definiert einen head Zeiger sowie einen current/end Zeiger. Diese beiden Zeiger erlauben ein schnelles Einfügen am Ende bzw. am Anfang der Liste.
template <typename data_t> class singleLinkedList { public: // Constructor for the list singleLinkedList() { head_ = 0; current_ = 0; } private: singleLinkedNode<data_t>* head_; singleLinkedNode<data_t>* current_; };Der Konstruktor der Liste setzt die beiden Element auf Null.
Als nächstes benötigen wir eine insert Funktion. Die Funktion fügt Elemente am Ende der Liste ein.
// Construtor // ... // ... // insert something into list void insert(data_t data) { if(head_== 0) { // list is empty // insert first element and point head and current to the new element head_ = new singleLinkedNode<data_t>(data); current_ = head_; } else { // something is in the list // insert a element at the end singleLinkedNode<data_t>* temp = new singleLinkedNode<data_t>(data); current_->next_ = temp; current_ = temp; /*** if you want to insert the element at the beginning do it like this head_ = temp; temp->next_ = data; ***/ } } // private SachenDie Funktion prüft ab ob die Liste leer ist. Wenn dass der Fall ist, wird ein neues Element in die Liste eingefügt, head_ wird auf das neue Element gebogen und current_ zeigt ebenfalls auf das Element.
Ist die Liste nicht leer wird ein neues Objekt erzeugt und current_->next_ wird auf das neue Element temp gebogen (Die Verknüpfung). Danach wird der eigentliche current_ Zeiger auf das neue Element gebogen.
Einfügen in eine leere Liste
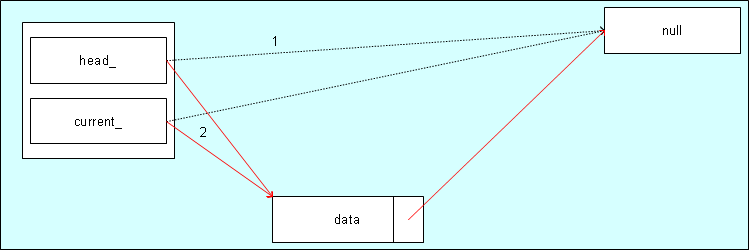
Der Anfangszustand ist mit (1) im Bild markiert. Nach dem Einfügen sieht es aus wie in Zustand (2).
Einfügen in eine nicht leere Liste.
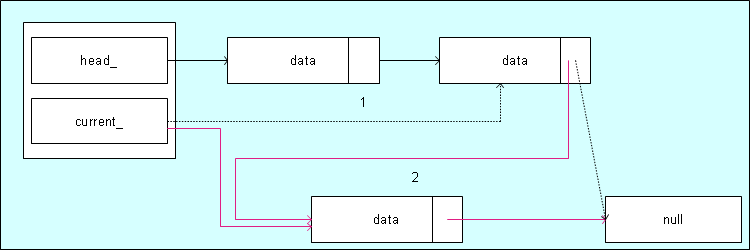
Der Anfangszustand (1) zeigt eine nicht leere Liste mit 2 Elementen. Zum Einfügen eines neuen Elements verbiegen wir den next Link des current/end Zeiger auf das neue Element und dann den current/end Zeiger selbst. Das verschafft uns den Endzustand (2). Zum Einfüge am Beginn der Liste kann man das ganze Spiel auch mit dem Head Zeiger betreiben. Wie dass funktioniert steht im Quelltext.
Soweit so gut. Da man hier aber mit new operiert, muss irgendwann einmal der Speicher aufgeräumt werden. Das erledigen wir im Destruktor der so aussehen könnte.
~singleLinkedList() { singleLinkedNode<data_t>* run, *del; run = head_; while(run != NULL) { del = run; run = run->next_; delete del; } }Der Destruktor läuft durch die Liste und löscht der Reihe nach ihre Elemente.
Als nächstes wäre es interessant zu sehen ob die ganze Konstruktion überhaupt funktioniert. Dazu schreiben wir eine ListOutput Funktion.
// Konstruktor // insert // Destructor // .. // .. void ListOutput() { singleLinkedNode<data_t>* run = head_; while(run != NULL) { std::cout << run->data_ << std::endl; run = run->next_; } } // private Deklarationen // ...Im Prinzip funktioniert die Ausgabefunktion wie der Destruktor. Wir laufen wieder durch die Liste. Nur diesmal geben wir die in der Liste vorhanden Daten aus.
Ein mögliches Testprogramm könnte so aussehen.
int main(void) { singleLinkedList<int> list; list.insert(1); list.insert(2); list.ListOutput(); std::cin.get(); return 0; }Natürlich braucht eine Liste noch mehr Funktionalität. Dazu gehören unter anderem Funktionen wie delete, deleteAt, find und getAt die wir als nächstes Implementieren.
....
FRAGE AN ALLE
Soll ich nen rekursiven Aufbau von Listen auch machen? So was in der Art wie
hier meine ich.template <typename data_> class MyList { public: MyList(data_ data, MyList<data_>* Tail = NULL) : head(data), tail(Tail){} MyList<data_>& insert(MyList<data_>& Tail) { tail = &Tail; return *this; } void Output() { MyList<data_>* run = this; while(run != NULL) { std::cout << run->head << std::endl; run = run->tail; } } data_ head; MyList* tail; }; int main() { MyList<int> a(0); MyList<int> b(1); MyList<int> c(2); a.insert(b.insert(c)); //a.Output(); MyList<int> d(3, &a); d.Output(); std::cin.get(); return 0; }Typlisten werden ja "ähnlich" aufgebaut...
FRAGE ENDE
-
Inhaltsverzeichnis
- Die einfach verkettete Liste
- Die doppelt verkettete Liste
- Typlisten
- Anwendungsgebiete
1 Die einfachverkettete Liste
Eine Liste besteht zunächst einmal aus Knoten die miteinander verknüpft werden. Eine Knotendefinition könnte so aussehen.
template <typename data_t> class singleLinkedNode { public: singleLinkedNode() : next_(0) {} singleLinkedNode(data_t data) : next_(0), data_(data) {} singleLinkedNode<data_t>* next_; data_t data_; };Wie man hier sieht, gibt es nur einen Next Zeiger. Das bedeutet dass der Knoten seinen Nachfolger, nicht aber seinen Vorgänger kennt.

Die Liste die diese Knotenstruktur verwaltet definiert einen head Zeiger sowie einen current/end Zeiger. Diese beiden Zeiger erlauben ein schnelles Einfügen am Ende bzw. am Anfang der Liste.
template <typename data_t> class singleLinkedList { public: // Constructor for the list singleLinkedList() { head_ = 0; current_ = 0; } private: singleLinkedNode<data_t>* head_; singleLinkedNode<data_t>* current_; };Der Konstruktor der Liste setzt die beiden Element auf Null.
Als nächstes benötigen wir eine insert Funktion. Die Funktion fügt Elemente am Ende der Liste ein.
// Construtor // ... // ... // insert something into list void insert(data_t data) { if(head_== 0) { // list is empty // insert first element and point head and current to the new element head_ = new singleLinkedNode<data_t>(data); current_ = head_; } else { // something is in the list // insert a element at the end singleLinkedNode<data_t>* temp = new singleLinkedNode<data_t>(data); current_->next_ = temp; current_ = temp; /*** if you want to insert the element at the beginning do it like this head_ = temp; temp->next_ = data; ***/ } } // private SachenDie Funktion prüft ab ob die Liste leer ist. Wenn dass der Fall ist, wird ein neues Element in die Liste eingefügt, head_ wird auf das neue Element gebogen und current_ zeigt ebenfalls auf das Element.
Ist die Liste nicht leer wird ein neues Objekt erzeugt und current_->next_ wird auf das neue Element temp gebogen (Die Verknüpfung). Danach wird der eigentliche current_ Zeiger auf das neue Element gebogen.
Einfügen in eine leere Liste

Der Anfangszustand ist mit (1) im Bild markiert. Nach dem Einfügen sieht es aus wie in Zustand (2).
Einfügen in eine nicht leere Liste.

Der Anfangszustand (1) zeigt eine nicht leere Liste mit 2 Elementen. Zum Einfügen eines neuen Elements verbiegen wir den next Link des current/end Zeiger auf das neue Element und dann den current/end Zeiger selbst. Das verschafft uns den Endzustand (2). Zum Einfüge am Beginn der Liste kann man das ganze Spiel auch mit dem Head Zeiger betreiben. Wie dass funktioniert steht im Quelltext.
Soweit so gut. Da man hier aber mit new operiert, muss irgendwann einmal der Speicher aufgeräumt werden. Das erledigen wir im Destruktor der so aussehen könnte.
~singleLinkedList() { singleLinkedNode<data_t>* run, *del; run = head_; while(run != NULL) { del = run; run = run->next_; delete del; } }Der Destruktor läuft durch die Liste und löscht der Reihe nach ihre Elemente.
Als nächstes wäre es interessant zu sehen ob die ganze Konstruktion überhaupt funktioniert. Dazu schreiben wir eine ListOutput Funktion.
// Konstruktor // insert // Destructor // .. // .. void ListOutput() { singleLinkedNode<data_t>* run = head_; while(run != NULL) { std::cout << run->data_ << std::endl; run = run->next_; } } // private Deklarationen // ...Im Prinzip funktioniert die Ausgabefunktion wie der Destruktor. Wir laufen wieder durch die Liste. Nur diesmal geben wir die in der Liste vorhanden Daten aus.
Ein mögliches Testprogramm könnte so aussehen.
int main(void) { singleLinkedList<int> list; list.insert(1); list.insert(2); list.ListOutput(); std::cin.get(); return 0; }Natürlich braucht eine Liste noch mehr Funktionalität. Dazu gehören unter anderem Funktionen wie delete, deleteAt, find und getAt die wir als nächstes Implementieren.
Um die Funktion delete zu implementieren schreiben wir uns zunächst ein Hilfsfunktion die uns das Element vor dem zu Löschenden zurückliefert. Dieses element brauchen wir um die Zeiger nach bzw. vor dem Löschen neu setzen zu können.
private: singleLinkedNode<data_t>* findItemBefore(data_t data) { singleLinkedNode<data_t>* run = head_; if(head_->data_ == data) { // Wenn head gesucht ist, head aushängen head_ = head_->next_; run->next_ = run; } else { while(run->next_ != NULL && run->next_->data_ != data) run = run->next_; } return run; }Zunächst prüfen wir ob head_ das zu löschende Element ist. Wenn das der Fall ist, schieben wir head auf das nächste Element und lassen run->next_ auf run zeigen. Damit ist das erste Element der Liste abgekoppelt und kann gelöscht werden.
Ansonsten laufen wir durch die Liste und schauen ob das nächste Element das gesuchte ist. Finden wir es nicht, steht run auf current_.
Warum liefern wir den current_ Zeiger zurück. Nunja, wir suchen schließlich das Element vor dem zu Löschenden. Und wenn wir dass zu löschende nicht finden löschen wir nichts, da current_->next_ auf NULL zeigt.
Den head_ aus der Liste auskoppeln
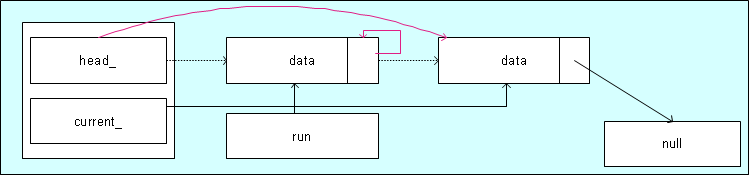
Die roten Pfeile verbildlichen das Auskoppeln des Kopfes der Liste. Da der run Zeiger nun mit next_ auf sich selbst zeigt, funktioniert der Code in der delete Funktion mit dem Kopf der Liste ebenso wie mit einem Element in der Liste.
bool deleteItem(data_t data) { singleLinkedNode<data_t> *del, *temp; temp = findItemBefore(data); del = temp->next_; if(del == NULL) return false; temp->next_ = del->next_; if (current_ == del) current_ = temp; delete del; return true; }Wir holen uns einen Zeiger auf das elment vor dem zu löschendem Element. Danach holen wir uns den Zeiger auf das zu löschende Element. Ist dieser NULL wurde das Element nicht gefunden und wir springen mit false aus der Funktion. Wenn nicht biegen wir die Zeiger um. Ist dass zu löschende Element dass current/end Element, schieben wir current_ um einen Position nach vorne. Zum Schluss wir der Speicher des zulöschenden Elements mit delete freigegeben.
Löschen in der Liste
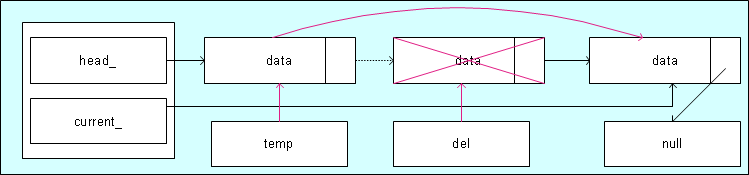
FRAGE AN ALLE
Soll ich nen rekursiven Aufbau von Listen auch machen? So was in der Art wie
hier meine ich.template <typename data_> class MyList { public: MyList(data_ data, MyList<data_>* Tail = NULL) : head(data), tail(Tail){} MyList<data_>& insert(MyList<data_>& Tail) { tail = &Tail; return *this; } void Output() { MyList<data_>* run = this; while(run != NULL) { std::cout << run->head << std::endl; run = run->tail; } } data_ head; MyList* tail; }; int main() { MyList<int> a(0); MyList<int> b(1); MyList<int> c(2); a.insert(b.insert(c)); //a.Output(); MyList<int> d(3, &a); d.Output(); std::cin.get(); return 0; }Typlisten werden ja "ähnlich" aufgebaut...
FRAGE ENDE
-
Inhaltsverzeichnis
- Die einfach verkettete Liste
- Die doppelt verkettete Liste
- Typlisten
- Anwendungsgebiete
1 Die einfachverkettete Liste
Eine Liste besteht zunächst einmal aus Knoten die miteinander verknüpft werden. Eine Knotendefinition könnte so aussehen.
template <typename data_t> class singleLinkedNode { public: singleLinkedNode() : next_(0) {} singleLinkedNode(data_t data) : next_(0), data_(data) {} singleLinkedNode<data_t>* next_; data_t data_; };Wie man hier sieht, gibt es nur einen Next Zeiger. Das bedeutet dass der Knoten seinen Nachfolger, nicht aber seinen Vorgänger kennt.

Die Liste die diese Knotenstruktur verwaltet definiert einen head Zeiger sowie einen current/end Zeiger. Diese beiden Zeiger erlauben ein schnelles Einfügen am Ende bzw. am Anfang der Liste.
template <typename data_t> class singleLinkedList { public: // Constructor for the list singleLinkedList() { head_ = 0; current_ = 0; length_ = 0; } private: singleLinkedNode<data_t>* head_; singleLinkedNode<data_t>* current_; int length_; };Der Konstruktor der Liste setzt die beiden Element auf Null.
Als nächstes benötigen wir eine insert Funktion. Die Funktion fügt Elemente am Ende der Liste ein.
// Construtor // ... // ... // insert something into list void insertItem(data_t data) { if(head_== 0) { // list is empty // insert first element and point head and current to the new element head_ = new singleLinkedNode<data_t>(data); current_ = &(*head_); } else { // something is in the list // insert a element at the end singleLinkedNode<data_t>* temp = new singleLinkedNode<data_t>(data); current_->next_ = temp; current_ = temp; /*** if you want to insert the element at the beginning do it like this head = temp; temp->next = data; ***/ } ++length_; // private SachenDie Funktion prüft ab ob die Liste leer ist. Wenn dass der Fall ist, wird ein neues Element in die Liste eingefügt, head_ wird auf das neue Element gebogen und current_ zeigt ebenfalls auf das Element.
Ist die Liste nicht leer wird ein neues Objekt erzeugt und current_->next_ wird auf das neue Element temp gebogen (Die Verknüpfung). Danach wird der eigentliche current_ Zeiger auf das neue Element gebogen.
Einfügen in eine leere Liste

Der Anfangszustand ist mit (1) im Bild markiert. Nach dem Einfügen sieht es aus wie in Zustand (2).
Einfügen in eine nicht leere Liste.

Der Anfangszustand (1) zeigt eine nicht leere Liste mit 2 Elementen. Zum Einfügen eines neuen Elements verbiegen wir den next Link des current/end Zeiger auf das neue Element und dann den current/end Zeiger selbst. Das verschafft uns den Endzustand (2). Zum Einfüge am Beginn der Liste kann man das ganze Spiel auch mit dem Head Zeiger betreiben. Wie dass funktioniert steht im Quelltext.
Soweit so gut. Da man hier aber mit new operiert, muss irgendwann einmal der Speicher aufgeräumt werden. Das erledigen wir im Destruktor der so aussehen könnte.
~singleLinkedList() { singleLinkedNode<data_t>* run, *del; run = head_; while(run != NULL) { del = run; run = run->next_; delete del; } }Der Destruktor läuft durch die Liste und löscht der Reihe nach ihre Elemente.
Als nächstes wäre es interessant zu sehen ob die ganze Konstruktion überhaupt funktioniert. Dazu schreiben wir eine ListOutput Funktion.
// Konstruktor // insert // Destructor // .. // .. void ListOutput() { singleLinkedNode<data_t>* run = head_; while(run != NULL) { std::cout << run->data_ << std::endl; run = run->next_; } } // private Deklarationen // ...Im Prinzip funktioniert die Ausgabefunktion wie der Destruktor. Wir laufen wieder durch die Liste. Nur diesmal geben wir die in der Liste vorhanden Daten aus.
Ein mögliches Testprogramm könnte so aussehen.
int main(void) { singleLinkedList<int> list; list.insert(1); list.insert(2); list.ListOutput(); std::cin.get(); return 0; }Natürlich braucht eine Liste noch mehr Funktionalität. Dazu gehören unter anderem Funktionen wie delete, deleteAt, find und getAt die wir als nächstes Implementieren.
Um die Funktion delete zu implementieren schreiben wir uns zunächst ein Hilfsfunktion die uns das Element vor dem zu Löschenden zurückliefert. Dieses element brauchen wir um die Zeiger nach bzw. vor dem Löschen neu setzen zu können.
private: singleLinkedNode<data_t>* findItemBefore(data_t data, int* countPos = NULL) { int counter = 0; singleLinkedNode<data_t>* run = head_; if(head_->data_ == data) { // Wenn head gesucht ist, head aushängen head_ = head_->next_; run->next_ = run; } else { while(run->next_ != NULL && run->next_->data_ != data) { run = run->next_; ++counter; } if(countPos != NULL) *countPos = counter+1; } return run; }Zunächst prüfen wir ob head_ das zu löschende Element ist. Wenn das der Fall ist, schieben wir head auf das nächste Element und lassen run->next_ auf run zeigen. Damit ist das erste Element der Liste abgekoppelt und kann gelöscht werden.
Ansonsten laufen wir durch die Liste und schauen ob das nächste Element das gesuchte ist. Finden wir es nicht, steht run auf current_.
Warum liefern wir den current_ Zeiger zurück. Nunja, wir suchen schließlich das Element vor dem zu Löschenden. Und wenn wir dass zu löschende nicht finden löschen wir nichts, da current_->next_ auf NULL zeigt.
Den head_ aus der Liste auskoppeln

Die roten Pfeile verbildlichen das Auskoppeln des Kopfes der Liste. Da der run Zeiger nun mit next_ auf sich selbst zeigt, funktioniert der Code in der delete Funktion mit dem Kopf der Liste ebenso wie mit einem Element in der Liste.
bool deleteItem(data_t data) { singleLinkedNode<data_t> *del, *temp; temp = findItemBefore(data); del = temp->next_; if(del == NULL) return false; temp->next_ = del->next_; if (current_ == del) current_ = temp; delete del; --length_; return true; }Wir holen uns einen Zeiger auf das elment vor dem zu löschendem Element. Danach holen wir uns den Zeiger auf das zu löschende Element. Ist dieser NULL wurde das Element nicht gefunden und wir springen mit false aus der Funktion. Wenn nicht biegen wir die Zeiger um. Ist dass zu löschende Element dass current/end Element, schieben wir current_ um einen Position nach vorne. Zum Schluss wir der Speicher des zulöschenden Elements mit delete freigegeben.
Löschen in der Liste

Als Letztes beschäftigen wir uns mit den Funktionen zum finden und holen der Elemente aus der Liste.
int findItem(data_t data) { singleLinkedNode<data_t> *finder; int count = 0; finder = findItemBefore(data, &count); finder = finder->next_; return count; }Die find Funktion bedient sich der findItemBefore Methode um dass Gesuchte Element zu finden. Als Rückgabewerte wird der Index zurückgeliefert. Bei einem nicht auffinden des Elements wird die Länge der Liste zurückgeliefert.
data_t* getItem(int index) { if(index >= length_) return NULL; singleLinkedNode<data_t>* finder = head_; int pos = 0; while(pos != index) { finder = finder->next_; ++pos; } return &finder->data_; }Die getItem Methode liefert einen Zeiger auf das gefundene Element an der Stelle Index. Sollte der index größer oder gleich der Länge der Liste sein wird NULL zurückgeliefert.
...
FRAGE AN ALLE
Soll ich nen rekursiven Aufbau von Listen auch machen? So was in der Art wie
hier meine ich.template <typename data_> class MyList { public: MyList(data_ data, MyList<data_>* Tail = NULL) : head(data), tail(Tail){} MyList<data_>& insert(MyList<data_>& Tail) { tail = &Tail; return *this; } void Output() { MyList<data_>* run = this; while(run != NULL) { std::cout << run->head << std::endl; run = run->tail; } } data_ head; MyList* tail; }; int main() { MyList<int> a(0); MyList<int> b(1); MyList<int> c(2); a.insert(b.insert(c)); //a.Output(); MyList<int> d(3, &a); d.Output(); std::cin.get(); return 0; }Typlisten werden ja "ähnlich" aufgebaut...
FRAGE ENDE