[A]Algorithmen/Datenstrukturen: Einfach-/Doppeltverkettete Listen

[evilissimo]

Also der Code deiner Rekursiven Liste gefällt mir nicht. (Das ist nur meine Meinung)

Ausserdem sieht das mehr nach nem Single Type Tuple aus

Eventuell kannst du anstatt der Rekursiven Liste eine vereinfachte implementation eines tuple zeigen.

Ich denke das es mit den TypListen am besten zusammen passt

Ach ja und warum ist eigentlich dein "int length_;" signed? Gibt es auch negative längen?

Besser wäre du würdest einen unsigned datentypen wie z.B. size_t nehmen.

BR
Vinzenz

PS: Ich habs nur kurz überflogen und das ist was mir so aufgefallen ist. Ich denke das ein paar Teile des Artikels der Code Qualität wegen etwas Überarbeitung brauchen könnten.

[Jester]

Vielleicht doch nochmal über eine zyklische Implementierung mit Dummy-Head nachdenken? Ich denke, das könnte *den* Unterschied zu den 1000 Tutorials, die es zum Thema schon gibt, darstellen. Insbesondere, weil zum Beispiel viele STL-Implementierungen das benutzen und eben nicht die (imo leider) weitverbreitete null-terminierte Variante.

[Tobias Gerg]

evilissimo schrieb:

Also der Code deiner Rekursiven Liste gefällt mir nicht. (Das ist nur meine Meinung)

Ausserdem sieht das mehr nach nem Single Type Tuple aus

Eventuell kannst du anstatt der Rekursiven Liste eine vereinfachte implementation eines tuple zeigen.

Ich denke das es mit den TypListen am besten zusammen passt

Ach ja und warum ist eigentlich dein "int length_;" signed? Gibt es auch negative längen?

Besser wäre du würdest einen unsigned datentypen wie z.B. size_t nehmen.

BR
Vinzenz

PS: Ich habs nur kurz überflogen und das ist was mir so aufgefallen ist. Ich denke das ein paar Teile des Artikels der Code Qualität wegen etwas Überarbeitung brauchen könnten.

Danke fürs Feedback

Mit der Überarbeitung hast du recht, dass mit den size_t wird natürlich auch noch geändert...

[Tobias Gerg]

Jester schrieb:

Vielleicht doch nochmal über eine zyklische Implementierung mit Dummy-Head nachdenken? Ich denke, das könnte *den* Unterschied zu den 1000 Tutorials, die es zum Thema schon gibt, darstellen. Insbesondere, weil zum Beispiel viele STL-Implementierungen das benutzen und eben nicht die (imo leider) weitverbreitete null-terminierte Variante.

Jup, dass ist ne Überlegung wert... Da mach ich mich am WE dran...

Gruß
Tobi

[Tobias Gerg]

So, auf Anregung von evilissimo und Jester hab ich den Code nochmal überarbeitet...

Ich bitte um Feedback zur einfach verketteten Liste.

[Tobias Gerg]

Inhaltsverzeichnis

• Die einfach verkettete Liste

• Definition

• Einfügen

• Finden

• Holen

• Löschen

• Destruktor und die Listenlänge

• Die doppelt verkettete Liste

• Typlisten

• Anwendungsgebiete

1 Die einfach verkettete Liste

Eine einfach verkettete Liste besteht aus Knoten die vorwärts miteinander verkettet sind. In den meisten Implementierungen, die man in Tutorials findet wird die Liste null terminiert. In diesem Artikel verwenden wir zur Endeerkennung ein anderes Verfahren.

Die folgenden Codefragmente sind in C++ geschrieben.

1.1 Definition der Liste

template <typename data_t>
class singleLinkedList
{
public:
	singleLinkedList() : head(new singleLinkedNode<data_t>()) , length(0)
	{
		// Constructor erzeugt Dummy head
		head->next = head;
	}

protected:

	template <typename data_t>
	class singleLinkedNode
	{};

	// Es darf nur Listknoten mit dem selben Typ wie in der Liste geben
	template<>
	class singleLinkedNode<data_t>
	{
	public:
		singleLinkedNode() : next(NULL) {}
		singleLinkedNode(data_t data) : data(data), next(NULL) {}

		singleLinkedNode* next;
		data_t data;
	};

private:
	singleLinkedNode<data_t>* head;
	size_t length;
};

Der Konstruktor der Liste erzeugt einen dummy head, der bei dieser Implementierung als Endeerkennung dient. Die Listdefinition ist außerdem zyklisch, da der "dummy" head wieder auf sich selbst zeigt.

Die Definition der Knoten wird in der Listenklasse versteckt, da die Knotendefinition von außen nicht sichtbar sein muss.

Das Einfügen in die Liste ist, da wir am Anfang der Liste einfügen schnell erledigt.

1.2 Einfügen eines Elements in die Liste

void insertItem(data_t d)
	{
		singleLinkedNode<data_t> *tmp = new singleLinkedNode<data_t>(d);
		//Neue Node einhängen
		tmp->next = head->next;
		head->next = tmp;

		//Länge erhöhen
		length++;
	}

Wie man im Code sieht, fügt man also immer vor dem head ein.

1.3 Finden eines Elements n der Liste

int  findItem(data_t d)
	{
		int index = 0;
		head->data = d;
		singleLinkedNode<data_t> *tmp = head->next;

		// Das Element vor dem zu suchenden Element finden
		while(tmp->data != d)
		{
			tmp = tmp->next;
			++index;
		}

		return ( index == length ? -1 : index);

	}

Man speichert das zu suchende Element, im head. Findet man das Element im head, ist die Länge zu groß. Genau auf diese Bedingung wird beim return geprüft.

1.4 Holen eines Elements aus der Liste

data_t* getItem(int index)
	{
		singleLinkedNode<data_t> *tmp = head;

		// Ausserhalb der Liste
		if(index < 0 || index >= static_cast<int>(length))
			return NULL;

		do
		{
			tmp = tmp->next;
			--index;
		}
		while(index >= 0);

		return &(tmp->data);

	}

Geholt wird ein Element über den Index (siehe findElement). Dabei ist immer zu beachten, dass wir am Beginn der Liste einfügen.

In der Funktion selbst prüfen wir den Range des Index. Ist der außerhalb der Liste, springen wir aus der Funktion.

Ansonsten holen wir index mal das nächste Element. Wegen dem Sonderfall index = 0 ist die Schleife eine do while Schleife.

1.5 Löschen eines Elements aus der Liste

void deleteItem(data_t d)
	{
		singleLinkedNode<data_t>*del, *tmp = head;

		// Zu löschendes Element suchen
		while(tmp->next != head && tmp->next->data != d)
			tmp = tmp->next;

		// Nicht gefunden return (könnte ein bool sein, dann return false)
		if(tmp->next == head)
			return;

		// Das zu löschende Element holen
		del = tmp->next;

		// Zeiger verbiegen
		tmp->next = tmp->next->next;

		// und löschen
		delete del;

		--length;

	}

Wir suchen zunächst das Element und merken uns den Vorgänger davon. Finden wir das Element nicht, springen wir aus der Funktion. Anderfalls verbiegen wir die Zeiger und löschen das Element.

1.6 Destruktor und die Listenlänge

~singleLinkedList()
	{
		// Destruktor zerstört alle Elemente in der liste incl. dummy head
		singleLinkedNode<data_t> *del = head->next, *tmp = head->next->next;

		// Solange Elemente in der Liste
		while(del != head)
		{
			//lösche gefundenes Element und gehe zum nächsten
			delete del;
			del = tmp;

			// Schützt vor weiterleitung auf ein gelöschtes Element
			if(tmp != head)
				tmp = tmp->next;
		}
		delete del;
		length = 0;

	}

	const size_t getLength()
	{
		return length;
	}

Im Destruktor löschen wir alle verbliebenen Elemente der Liste einschließlich dem head.

Die Längenfunktion ist ein simpler return der aktuellen Länge.

Bilder von der Neuimplementierung werden noch nachgeliefert....
Bitte um Feedback zum Code.

[Jester]

Zur Suche:

wie wär's mit folgender Implementierung

int  findItem(data_t d)
{
  head->data = d; // sentinel plazieren
  singleLinkedNode<data_t> * p = head->next;
  int pos = 0;

  while(p->data != d){
    p = p->next; ++pos;
  }

  return pos;
}

bzw. am schluß noch abprüfen, ob die zahl zu groß ist und -1 zurückgeben. Wenn man Iteratoren implementiert und den Iterator, der auf den head zeigt als end benutzt, dann kriegt man damit sogar automatisch den end-iterator zurück, wenn das datum nicht in der liste ist.

[Tobias Gerg]

Stimmt, die Idee mit dem Sentinel ist nicht übel... Bau ich gleich noch mit ein...

Gruß
Tobi

[Tobias Gerg]

Inhaltsverzeichnis

• Die einfach verkettete Liste

• Definition

• Einfügen

• Finden

• Holen

• Löschen

• Destruktor und die Listenlänge

• Die doppelt verkettete Liste

• Typlisten

• Anwendungsgebiete

1 Die einfach verkettete Liste

Eine einfach verkettete Liste besteht aus Knoten die vorwärts miteinander verkettet sind. In den meisten Implementierungen, die man in Tutorials findet wird die Liste null terminiert. In diesem Artikel verwenden wir zur Endeerkennung ein anderes Verfahren.

Die folgenden Codefragmente sind in C++ geschrieben.

1.1 Definition der Liste

template <typename data_t>
class singleLinkedList
{
public:
	singleLinkedList() : head(new singleLinkedNode<data_t>()) , length(0)
	{
		// Constructor erzeugt Dummy head
		head->next = head;
	}

protected:

	template <typename data_t>
	class singleLinkedNode
	{};

	// Es darf nur Listknoten mit dem selben Typ wie in der Liste geben
	template<>
	class singleLinkedNode<data_t>
	{
	public:
		singleLinkedNode() : next(NULL) {}
		singleLinkedNode(data_t data) : data(data), next(NULL) {}

		singleLinkedNode* next;
		data_t data;
	};

private:
	singleLinkedNode<data_t>* head;
	size_t length;
};

Der Konstruktor der Liste erzeugt einen dummy head, der bei dieser Implementierung als Endeerkennung dient. Die Listdefinition ist außerdem zyklisch, da der "dummy" head wieder auf sich selbst zeigt.

Die Definition der Knoten wird in der Listenklasse versteckt, da die Knotendefinition von außen nicht sichtbar sein muss.

Das Einfügen in die Liste ist, da wir am Anfang der Liste einfügen schnell erledigt.

1.2 Einfügen eines Elements in die Liste

void insertItem(data_t d)
	{
		singleLinkedNode<data_t> *tmp = new singleLinkedNode<data_t>(d);
		//Neue Node einhängen
		tmp->next = head->next;
		head->next = tmp;

		//Länge erhöhen
		length++;
	}

Wie man im Code sieht, fügt man also immer vor dem head ein.

1.3 Finden eines Elements n der Liste

int  findItem(data_t d)
	{
		int index = 0;
		head->data = d;
		singleLinkedNode<data_t> *tmp = head->next;

		// Das Element vor dem zu suchenden Element finden
		while(tmp->data != d)
		{
			tmp = tmp->next;
			++index;
		}

		return ( index == length ? -1 : index);

	}

Man speichert das zu suchende Element, im head. Findet man das Element im head, ist die Länge zu groß. Genau auf diese Bedingung wird beim return geprüft.

1.4 Holen eines Elements aus der Liste

data_t* getItem(int index)
	{
		singleLinkedNode<data_t> *tmp = head;

		// Ausserhalb der Liste
		if(index < 0 || index >= static_cast<int>(length))
			return NULL;

		do
		{
			tmp = tmp->next;
			--index;
		}
		while(index >= 0);

		return &(tmp->data);

	}

Geholt wird ein Element über den Index (siehe findElement). Dabei ist immer zu beachten, dass wir am Beginn der Liste einfügen.

In der Funktion selbst prüfen wir den Range des Index. Ist der außerhalb der Liste, springen wir aus der Funktion.

Ansonsten holen wir index mal das nächste Element. Wegen dem Sonderfall index = 0 ist die Schleife eine do while Schleife.

1.5 Löschen eines Elements aus der Liste

void deleteItem(data_t d)
	{
		singleLinkedNode<data_t>*del, *tmp = head;

		// Zu löschendes Element suchen
		while(tmp->next != head && tmp->next->data != d)
			tmp = tmp->next;

		// Nicht gefunden return (könnte ein bool sein, dann return false)
		if(tmp->next == head)
			return;

		// Das zu löschende Element holen
		del = tmp->next;

		// Zeiger verbiegen
		tmp->next = tmp->next->next;

		// und löschen
		delete del;

		--length;

	}

Wir suchen zunächst das Element und merken uns den Vorgänger davon. Finden wir das Element nicht, springen wir aus der Funktion. Anderfalls verbiegen wir die Zeiger und löschen das Element.

1.6 Destruktor und die Listenlänge

~singleLinkedList()
	{
		// Destruktor zerstört alle Elemente in der liste incl. dummy head
		singleLinkedNode<data_t> *del = head->next, *tmp = head->next->next;

		// Solange Elemente in der Liste
		while(del != head)
		{
			//lösche gefundenes Element und gehe zum nächsten
			delete del;
			del = tmp;

			// Schützt vor weiterleitung auf ein gelöschtes Element
			if(tmp != head)
				tmp = tmp->next;
		}
		delete del;
		length = 0;

	}

	const size_t getLength()
	{
		return length;
	}

Im Destruktor löschen wir alle verbliebenen Elemente der Liste einschließlich dem head.

Die Längenfunktion ist ein simpler return der aktuellen Länge.

Bilder von der Neuimplementierung werden noch nachgeliefert....
Bitte um Feedback zum Code.

[Tobias Gerg]

Inhaltsverzeichnis

• Die einfach verkettete Liste

• Definition

• Einfügen

• Finden

• Holen

• Löschen

• Destruktor und die Listenlänge

• Die doppelt verkettete Liste

• Definition

• Einfügen

• Finden

• Löschen

• Destruktor und die Listenlänge

• Typlisten

• Rekursive Datentypen

• Listen von Datentypen

• Operationen auf Typlisten

• Anwendungsgebiete

1 Die einfach verkettete Liste

Eine einfach verkettete Liste besteht aus Knoten die vorwärts miteinander verkettet sind. In den meisten Implementierungen, die man in Tutorials findet wird die Liste null terminiert. In diesem Artikel verwenden wir zur Endeerkennung ein anderes Verfahren.

Die folgenden Codefragmente sind in C++ geschrieben.

1.1 Definition der Liste

template <typename data_t>
class singleLinkedList
{
public:
	singleLinkedList() : head(new singleLinkedNode<data_t>()) , length(0)
	{
		// Constructor erzeugt Dummy head
		head->next = head;
	}

protected:

	template <typename data_t>
	class singleLinkedNode
	{};

	// Es darf nur Listknoten mit dem selben Typ wie in der Liste geben
	template<>
	class singleLinkedNode<data_t>
	{
	public:
		singleLinkedNode() : next(NULL) {}
		singleLinkedNode(data_t data) : data(data), next(NULL) {}

		singleLinkedNode* next;
		data_t data;
	};

private:
	singleLinkedNode<data_t>* head;
	size_t length;
};

Der Konstruktor der Liste erzeugt einen dummy head, der bei dieser Implementierung als Endeerkennung dient. Die Listdefinition ist außerdem zyklisch, da der "dummy" head wieder auf sich selbst zeigt.

Die Definition der Knoten wird in der Listenklasse versteckt, da die Knotendefinition von außen nicht sichtbar sein muss.

Das Einfügen in die Liste ist, da wir am Anfang der Liste einfügen schnell erledigt.

1.2 Einfügen eines Elements in die Liste

void insertItem(data_t d)
	{
		singleLinkedNode<data_t> *tmp = new singleLinkedNode<data_t>(d);
		//Neue Node einhängen
		tmp->next = head->next;
		head->next = tmp;

		//Länge erhöhen
		length++;
	}

Wie man im Code sieht, fügt man also immer vor dem head ein.

1.3 Finden eines Elements n der Liste

int  findItem(data_t d)
	{
		int index = 0;
		head->data = d;
		singleLinkedNode<data_t> *tmp = head->next;

		// Das Element vor dem zu suchenden Element finden
		while(tmp->data != d)
		{
			tmp = tmp->next;
			++index;
		}

		return ( index == length ? -1 : index);

	}

Man speichert das zu suchende Element, im head. Findet man das Element im head, ist die Länge zu groß. Genau auf diese Bedingung wird beim return geprüft.

1.4 Holen eines Elements aus der Liste

data_t* getItem(int index)
	{
		singleLinkedNode<data_t> *tmp = head;

		// Ausserhalb der Liste
		if(index < 0 || index >= static_cast<int>(length))
			return NULL;

		do
		{
			tmp = tmp->next;
			--index;
		}
		while(index >= 0);

		return &(tmp->data);

	}

Geholt wird ein Element über den Index (siehe findElement). Dabei ist immer zu beachten, dass wir am Beginn der Liste einfügen.

In der Funktion selbst prüfen wir den Range des Index. Ist der außerhalb der Liste, springen wir aus der Funktion.

Ansonsten holen wir index mal das nächste Element. Wegen dem Sonderfall index = 0 ist die Schleife eine do while Schleife.

1.5 Löschen eines Elements aus der Liste

void deleteItem(data_t d)
	{
		singleLinkedNode<data_t>*del, *tmp = head;

		// Zu löschendes Element suchen
		while(tmp->next != head && tmp->next->data != d)
			tmp = tmp->next;

		// Nicht gefunden return (könnte ein bool sein, dann return false)
		if(tmp->next == head)
			return;

		// Das zu löschende Element holen
		del = tmp->next;

		// Zeiger verbiegen
		tmp->next = tmp->next->next;

		// und löschen
		delete del;

		--length;

	}

Wir suchen zunächst das Element und merken uns den Vorgänger davon. Finden wir das Element nicht, springen wir aus der Funktion. Anderfalls verbiegen wir die Zeiger und löschen das Element.

1.6 Destruktor und die Listenlänge

~singleLinkedList()
	{
		// Destruktor zerstört alle Elemente in der liste incl. dummy head
		singleLinkedNode<data_t> *del = head->next, *tmp = head->next->next;

		// Solange Elemente in der Liste
		while(del != head)
		{
			//lösche gefundenes Element und gehe zum nächsten
			delete del;
			del = tmp;

			// Schützt vor weiterleitung auf ein gelöschtes Element
			if(tmp != head)
				tmp = tmp->next;
		}
		delete del;
		length = 0;

	}

	const size_t getLength()
	{
		return length;
	}

Im Destruktor löschen wir alle verbliebenen Elemente der Liste einschließlich dem head.

Die Längenfunktion ist ein simpler return der aktuellen Länge.

2 Die doppelt verkettete Liste

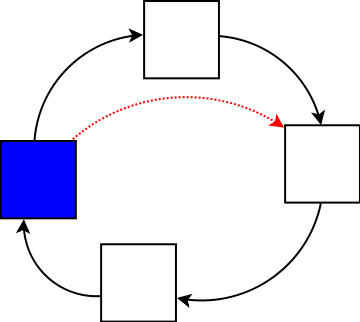
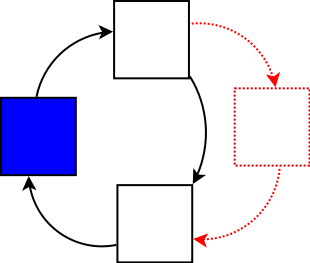
Die doppelt verkettete Liste hat zusätzlich zum next Zeiger auch einen back zeiger.

2.1 Definition

template <typename data_t>
class doubleLinkedList
{
public:
    doubleLinkedList() : head(new doubleLinkedNode<data_t>()) , length(0)
    {
        // Constructor erzeugt Dummy head
        head->next = head;
	head->back = head;
    }

protected:

    template <typename data_t>
    class doubleLinkedNode
    {};

    // Es darf nur Listknoten mit dem selben Typ wie in der Liste geben
    template<>
    class doubleLinkedNode<data_t>
    {
    public:
        doubleLinkedNode() : next(NULL) {}
        doubleLinkedNode(data_t data) : data(data), next(NULL), back(NULL) {}

        doubleLinkedNode* next;
	doubleLinkedNode* back;

        data_t data;
    };

private:
    doubleLinkedNode<data_t>* head;
    size_t length;
};

Die Definition ist von der einfach verketteten Liste schon bekannt. Einzig der back zeiger in der doubleLinkedNode ist hinzugekommen.

2.2 Einfügen die Liste

void insertItem(data_t d)
    {
        doubleLinkedNode<data_t> *tmp = new doubleLinkedNode<data_t>(d);
	tmp->next = head;
	tmp->back = head->back;

	head->back->next = tmp;
	head->back = tmp;
	this->length++;
    }

Beim Einfügen (hier ein back insert) wird zunächst das neue Element mit der Liste verknüpft. Danach wird Über den back Zeiger das Element in die Liste hinzugefügt.

[Bild]

2.3 Finden eines Elements in der Liste

data_t* findItem(data_t d)
    {

        doubleLinkedNode<data_t> *forward = head->next, *backward=head->back;

        // Das Element vor dem zu suchenden Element finden
        while(forward->data != d && 
	      backward->data != d)
        {
		if(forward->next == backward)
			return NULL;

		forward = forward->next;
		backward = backward->back;

        }

	return (forward->data == d) ? &(forward->data) : &(backward->data);

    }

Im Gegensatz zur Implementierung bei der einfach verketteten Liste erledigen wir in dieser Implementierung das finden und holen aus der Liste in einer Funktion.

Das gesuchte Element wird von hinten und vorne gesucht. Findet man das Element gibt man einen Zeiger auf die Daten im Knoten zurück, ansonsten wird ein Null Zeiger zurückgegeben.

[Bild]

2.4 Löschen aus der Liste

bool deleteItem(data_t item)
{
        doubleLinkedNode<data_t>*del, *forward = head->next, *backward=head->back;

        // Das Element vor dem zu suchenden Element finden
        while(forward->data != item && 
			 backward->data != item)
        {
		if(forward->next == backward)
			return false;

		forward = forward->next;
		backward = backward->back;

        }

	del = (item == forward->data) ? forward : backward;
	del->back->next = del->next;
	del->next->back = del->back;

	return true;
}

Wiederum suchen wir das Element. Finden wir das Element hängen wir es aus und löschen es. Desweiteren geben wir true zurück. Wird das Element nicht gefunden wird false zurückgegeben.

[bild]

2.5 Destruktor und Längenfunktion

~doubleLinkedList()
    {
        // Destruktor zerstört alle Elemente in der liste incl. dummy head
        doubleLinkedNode<data_t> *del = head->next;

        // Solange Elemente in der Liste
        while(del != head)
        {
            //lösche gefundenes Element und gehe zum nächsten
            del = del->next;
	    delete del->back;

        }
        delete del;
        length = 0;

    }

Der Destruktor gibt den restlichen reservierten Speicher frei. Die Längen funktion kann aus der singleLinkedList entnommen werden.

3 Typlisten

3.1 Rekursive Datentypen

Nun kann man Listen auch als Rekursiven Datentyp auffassen.
Sie besteht aus einem Kopf und einer Restliste.

Diese Struktur kann man über Tupel realisieren.
Bitte um Feedback zum Code.