5. [A] Simulink

[A] Simulink

  • ?

    Bisher nur temporäres Zeugs, Feedback sinnfrei.

    TAG_BEGIN

    1 Einleitung

    Simulink ist eine Umgebung zur grafischen Modellierung von Systemen. Dabei ist es ein Aufsatz für Matlab(tm), weswegen es auch häufig als Matlab/Simulink(tm) bezeichnet wird. Obwohl sich Simulink(tm)
    nicht nur für die Modellierung technischer Systeme eignet, ist dies dennoch das häufigste Einsatzgebiet und deswegen liegt auch der Fokus dieses Artikels auf eben solchen.

    Die modellierten Systeme können direkt in Simulink simuliert werden. Es gibt gibt aber auch Erweiterungen mit welchen Quellcode, in der Regel C, für ein bestimmtes Zielsystem, genannt Target, generiert werden kann. Dieser Artikel beschränkt sich auf die Simulation. Vielmehr soll die Arbeitsweise mit dem Werkzeug anhand von kleinen aber realen Anwendungsbeispielen vorgestellt werden. Ganz ohne mathematische, signaltechnische Grundlagen geht dies zwar nicht, es wird aber auf ausführliche Herleitungen verzichtet.

    2 Grundlagen

    2.1 Differenzierung kontinuierlich/diskret

    Analoge Signale (z.B. Spannungen) sind wert-und zeitkontinuierlich. Das heisst, dass ein analoges Signal zu jedem Zeitpunkt t jeden möglichen Wert x(t) haben kann.


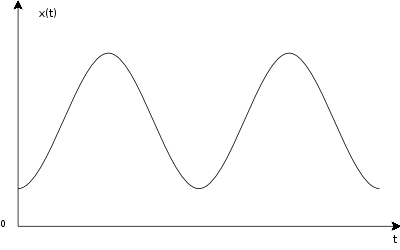
    Bild 2.1-1: Signal zeit- und wertkontinuierlich

    Dies kann ein digital arbeitender Rechner nicht verarbeiten, die Signale werden mit einem Analog/Digital-Wandler in ein dem Computer verständliches Format gewandelt.
    Zuerst wird das Signal durch den Abtastvorgang diskretisiert. Dabei wird vom A/D-Wandler zu bestimmten (in der Regel äquidistanten) Zeitpunkten der Wert des analogen Signals abgetastet (sampling). Dadurch wird das Signal zeitdiskret, bleibt aber immer noch wertkontinuierlich.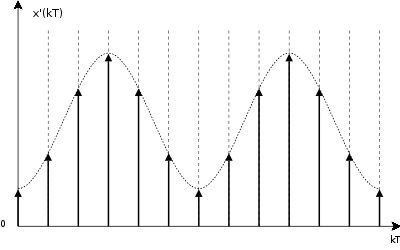


    Bild 2.1-2: Signal zeitdiskret, wertkontinuierlich

    Durch die abschliessende Wandlung wird nun der Wertebereich eingeschränkt, quantisiert.


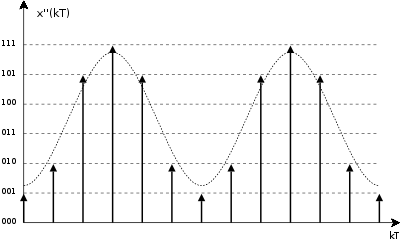
    Bild 2.1-3: Signal zeit-und wertdiskret

    TAG_END

    Ein paar Formeln...
    H(s)=ω_c2s2+ω_cQ∞s+ωc2H(s) = \frac{\omega\_c^2}{s^2 + \frac{\omega\_c}{Q_\infty}s + \omega_c^2}

    H(z)=a_0+a_1z−1+a_2z−21+b_1z−1+b2z−2H(z) = \frac{a\_0 + a\_1 z^{-1} + a\_2 z^{-2}}{1 + b\_1 z^{-1} + b_2 z^{-2}}

    K=tan(ω_cT_s2)K = \tan\left(\frac{\omega\_cT\_s}{2}\right)

    a0=K21+2K+K2a_0 = \frac{K^2}{1+\sqrt{2}K + K^2}

    a1=2K21+2K+K2a_1 = \frac{2K^2}{1+\sqrt{2}K + K^2}

    a2=K21+2K+K2a_2 = \frac{K^2}{1+\sqrt{2}K + K^2}

    b1=2(K2−1)1+2K+K2b_1 = \frac{2(K^2-1)}{1+\sqrt{2}K + K^2}

    b2=1−2K+K21+2K+K2b_2 = \frac{1- \sqrt{2}K + K^2}{1+\sqrt{2}K + K^2}

    ω_c=2π⋅f_c\omega\_c = 2\pi\cdot f\_c

    Ein bißchen Code...

    [i]% sample time and frequency[/i]

t_sample = 0.01;
f_sample = 1 / t_sample;

[i]% filter design values[/i]

omega_c = 2;

[i]% calculation of intermediate values
[/i]
K = tan( (omega_c * t_sample) / 2 );
coeff_denom = 1 + (sqrt(2) * K) + (K^2);

[i]% calculation of filter coefficients[/i]

a0 = K^2 / coeff_denom;
a1 = 2 * a0;
a2 = a0;

b1 = (2 * (K^2 - 1)) / coeff_denom;
b2 = (1 - (sqrt(2) * K) + K^2) / coeff_denom;

    Mal ein Bild...

    0
  • M

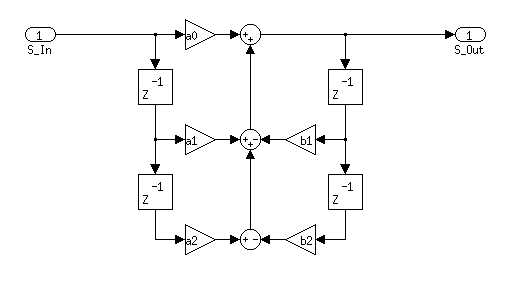
    beahndelst du die S-Functions oder "nur" die Simulationsoberflaeche

    0
  • ?

    mosta schrieb:

    beahndelst du die S-Functions oder "nur" die Simulationsoberflaeche

    In diesem Artikel werde ich definitiv nur die normale Oberfläche behandeln. S-Functions werden bestimmt kurz erwähnt, aber mehr nicht. Wieso? Willst einen Artikel dazu schreiben? *g*

    0
  • M

    Wenn man irgendwan mal wieder zeit hat dann schon aber eher nicht

    0
Anmelden zum Antworten