A Random Article: Die Mathematik hinter den Zufallszahlen
-
Dieser Artikel entspricht in leicht abgewandelter Form meiner Facharbeit im Bereich Mathematik, ist also primär nicht für Programmierer geschrieben worden. Allerdings ist gerade in mathematisch geprägten Bereichen wie dem der Pseudozufallszahlen ein gewisses Hintergrundwissen durchaus von Vorteil.
1 Motivation
Zufallszahlen sind aus vielen Anwendungsgebieten heute nicht mehr wegzudenken. Ihr vielfältiger Nutzen reicht von naturwissenschaftlichen Simulationen über Kryptographie und Computerspiele bis hin zur numerischen Analyse (es sei hier auf das Feld der Monte-Carlo-Algorithmen verwiesen, mit denen komplexe mathematische Zusammenhänge durch eine ausreichend große Menge zufälliger Zahlen analysiert werden können) oder Eingabesimulationen zum Testen von Software.
Es gibt gute, nicht voraussagbare natürliche Quellen für Zufallszahlen. So kann man z. B. die von einem Geigerzähler gelieferte Zahl radioaktiver Zerfälle innerhalb eines Zeitintervalls als zufällig betrachten oder das Rauschen in der Atmosphäre. Hier spricht man von nichtdeterministischen Zufallsgeneratoren, da die nächste Zufallszahl nicht vorhersehbar ist. Diese Generatoren haben allerdings entscheidende Nachteile für den täglichen Gebrauch:
- Die Zufallszahlen können nicht reproduziert werden, was vor allem bei wissenschaftlichen Experimenten unabdingbar ist. Auch sind moderne Computerspiele auf diesen Aspekt angewiesen. Denn wenn Objekte wie etwa Karten in einem Netzwerkspiel zufällig ausgewählt werden sollen, spart man Datentransfers über das relativ langsame Netzwerk und damit Zeit, indem man lediglich einen "Seed", d. h. einen Anfangswert für einen Zufallsgenerator, übermittelt.
- Sie sind oft nicht schnell genug (v. a. wenn die Daten über das Internet auf einen Computer übertragen werden).
- Sie stehen nicht jedem zur Verfügung.
Aus diesen Gründen gibt es Algorithmen, die Zufallszahlen erzeugen können. Dies ist erst einmal ein Widerspruch in sich: Ein Computer ist von Natur aus deterministisch. Wie soll eine solche Maschine etwas Zufälliges erzeugen können?
Die Lösung besteht darin, Algorithmen zu entwickeln, die nur scheinbar zufällige Zahlen erzeugen (Pseudozufallszahlen). Diese Arbeit gibt einen kurzen Einblick in den Themenkomplex der Pseudozufallszahlen mit den drei Schwerpunkten Erzeugen von Zufallszahlen, Ändern der Wahrscheinlichkeitsverteilung und Testen der Güte von Zufallsgeneratoren.
2 Zufallsgeneratoren
Wenn man einen Algorithmus zur Erzeugung von Zufallszahlen entwickeln möchte, ist es anfangs verlockend, diesen möglichst kompliziert zu halten, in der Hoffnung, die resultierenden Daten würden dadurch irgendwie zufälliger. Es hat sich jedoch in der Praxis bewährt, relativ einfache Algorithmen zu verwenden, da man diese deutlich besser (theoretisch) untersuchen und somit ihre Parameter besser einstellen kann, um der erzeugten Zahlenfolge gute Eigenschaften zu geben.
Weiterhin ist es sinnvoll, sich bei der Erzeugung von Zufallszahlen auf die Gleichverteilung zu beschränken. Dies hat zwei Gründe: Zum einen sind nur wenige hinreichend gute Algorithmen bekannt, die eine andere Verteilung zu eigen haben (sie sind komplexer und/ oder langsamer). Zum anderen gibt es gute und schnelle Möglichkeiten, die Gleichverteilung in andere Verteilungen umzuwandeln (s. dazu Kapitel 3).
Es gibt viele verschiedene Zufallsgeneratoren, die alle ihre Vor- und Nachteile haben. Bekannte sind der lineare Kongruenzgenerator, der inverse Kongruenzgenerator, der Fibonacci-Generator (nach der gleichnamigen Folge), der Blum-Blum-Shub-Generator, der v. a. in der Kryptographie beliebt ist, und der 1997 vorgestellte Mersenne-Twister, der wohl beste bekannte Zufallsgenerator.
2.1 Linearer Kongruenzgenerator
2.1.1 Einführung
Der lineare Kongruenzgenerator ist wohl der am häufigsten verwendete Zufallsgenerator. Er wurde 1949 von Derrick H. Lehmer entwickelt [Leh51, S. 141 - 146] und vereint hinreichende Zufälligkeit für die meisten, alltäglichen Anwendungsfälle mit sehr großer Geschwindigkeit und Simplizität. Nach der Festlegung der folgenden Parameter generiert er ganze Zahlen im Intervall
[0;m[:- das Modul $m,, m 0$
- der Faktor
- das Inkrement $c,, c m$
- der Startwert
- m, a, c, X_0 \in \mathds Z
Die nächste Zufallszahl wird dann nach der Vorschrift
X_{n + 1} = (aX_n + c) \mod m, \qquad n \geq 0
berechnet. Das
(n + k)-te Folgenglied lässt sich nach Verallgemeinerung von voriger Gleichung folgendermaßen ermitteln:X_{n + k} = \left(a^k X_n + (a^k - 1) \frac{c}{a - 1}\right) \mod m, \qquad n \geq 0,\, k \geq 0.
Da die Berechnung des Nachfolgers einer Zufallszahl eindeutig ist, handelt es sich beim linearen Kongruenzgenerator um eine Funktion. Auf Grund der durch das Modul eingeschränkten Definitions- und Wertemenge muss jede erzeugte Sequenz für jede beliebige Parameterkombination ab einer gewissen Stelle μ mit
0 [e]le[/e] [e]mu[/e] < mperiodisch sein, da nach(m - 1)Schritten kein noch nicht verwendeter Funktionswert mehr übrig ist, sodass eine Wiederholung unausweichlich ist. Die Periodenlänge λ liegt mit gleicher Argumentation zwischen1undm. Wann der maximal mögliche Fall[e]lambda[/e] = meintritt, beschreibt der Satz von Knuth:Satz von Knuth schrieb:
Die maximal mögliche Periodenlänge
[e]lambda[/e] = mwird genau dann erreicht, wenncteilerfremd zumist;a - 1durch jeden Primfaktor vonmteilbar ist;a - 1ein Vielfaches von4ist, wennmein Vielfaches von4ist.
[Knu97, S. 17 - 19]
Natürlich sind nicht alle übrigen Wahlen für die unterschiedlichen Parameter günstig, z. B. ergibt
a = 0odera = 1wenig Sinn, da die Erzeugungsformel so zuX_{n + 1} = c \mod m
bzw.
X_{n + 1} = (X\_n + c) \mod m = (X\_0 + nc) \mod m
vereinfacht würde. Die Parameter müssen des Weiteren aufeinander abgestimmt sein, um eine zufriedenstellende Folge an Zufallszahlen erstellen zu können. Eine umfassende Abhandlung über diese Zusammenhänge würde den Rahmen dieser Arbeit sprengen. Deshalb beschränke ich mich (neben dem oben erwähnten Satz von Knuth) auf eine kurze Behandlung des Moduls.
2.1.2 Wahl des Moduls
Das Modul
mbesitzt eine bedeutende und offensichtliche Rolle für die Güte eines linearen Kongruenzgenerators, weil es die maximal mögliche Periodenlänge bestimmt (s. o.). Ist diese zu kurz, d. h. ist die Zahl der im Anwendungsfall benötigten Zufallszahlen nicht mehr klein gegenüber[e]lambda[/e], kann die erzeugte Folge nicht mehr als hinreichend zufällig angesehen werden. Dieser Überlegung folgend, sollte das Modulmkeinesfalls dem Intervall angepasst werden, in dem die Zufallszahlen des Anwendungsfalls liegen sollen. Bräuchte man z. B. für Ja-Nein-Entscheidungen Zahlen im Intervall[0;1]und wählte deswegen das Modulm = 2, so wäre die maximal mögliche Periodenlänge[e]lambda[/e]ebenfalls2.Naheliegend für den Einsatz an einem Binärcomputer ist die Wahl des Moduls
m = 2^u, u \in \mathds N,
weil der Algorithmus so erheblich beschleunigt werden kann. Denn das Bilden des Restwerts ist allgemein eine relativ langsame Operation. Ist das Modul allerdings eine Potenz von
2, erhält man dasselbe Ergebnis, wenn man nur die letztenuBits betrachtet. Dies erreicht man mit einem bitweisen Und mit2^u - 1als zweitem Operanden.Ein Beispiel:
105 \mod 16 &= 105 \mod 2^4\\ &= 105 \text{ AND } (2^4 - 1)\\ &= 0110\, 1001\_b \text{ AND } 0000\, 1111\_b\\ &= 0000\, 1001_b\\ &= 9Wählt man als Modul
m = 2^umituals Registerbreite, wird sogar automatisch auf jede Operation die Modulofunktion angewendet, da nur die letztenuBits des Ergebnisses gespeichert werden können.So einfach diese Lösung wäre, praktikabel ist sie wegen eines allgemeinen Problems leider nicht: Wenn
dein Teiler vonmist undY[t]n[/t]durchY\_n = X\_n \mod d
beschrieben wird, dann gilt:
Y_{n + 1} = (aY_n + c) \mod d [Knu97, S. 13]
Das hat zur Folge, dass die niederwertigen Bits eine stark verkürzte Periode haben, weil die Anzahl der verschiedenen Zustände der letzten
uBits und damitdgleich2^uist und somitmteilt. Also haben beispielsweise die letzten drei Stellen eine maximale Periodenlänge von2^3 = 8.Zum Beseitigen dieses unschönen Effekts werden meist gleich zwei Tricks verwendet:
- Verwerfen der niederwertigen Bits
- Wahl des Moduls
m = 2^u - 1
Der erste Punkt ist selbsterklärend. Wenn ein Register mehr Bits hat als für das Intervall, in dem die Zufallszahlen liegen sollen, benötigt werden, werden nur die höchstwertigen Bits verwendet, da diese nicht der verkürzten Periode unterliegen. Der zweite Punkt bedient sich eines Rechentricks:
Wenn
m = 2^u - 1ist, wählt man am besten das Inkrementc = 0[Knu97, S. 12]. Somit verkürzt sich der Generator aufX_{n + 1} = aX_n \mod (2^u - 1)
Es seien nun
w := 2^u,\, q := \left\lfloor \frac{aX\_n}{w} \right\rfloor,\, r := aX\_n \mod w
definiert. Dann gilt:
aX_n \mod (w - 1) &= (qw + r) \mod (w - 1)\\ &= (qw - q + q + r) \mod (w - 1)\\ &= (q(w - 1) + q + r) \mod (w - 1)\\ &= (q + r) \mod (w - 1)\\ &= \begin{cases} q + r, &\text{wenn } q + r < w - 1\\ q + r - w + 1, &\text{wenn } q + r \geq w - 1 \end{cases}Letzteres ist gültig, da nach der Definition
q + r < 2(w - 1)sein muss [Knu97, S. 12 - 13]. Teiler von ausgewählten2^u - 1sind in dieser Tabelle verzeichnet [Knu97, S. 14]Ein für die Praxis relevanter Rechentrick ist der Schrage-Algorithmus [Sch79, S. 132 - 138]. Das Problem: Da eine möglichst große Periode für die Reihe der Zufallszahlen erreicht werden soll, ist
mmeist nicht mehr klein gegenüber dem maximal speicherbaren Wert. Bei der MultiplikationaX[t]n[/t]kann somit ein Wert erreicht werden, der zu groß ist, um gespeichert werden zu können. Es würde aber genügen, nuraX mod mauszurechnen, das genaue Produkt interessiert nicht. Hier setzt der Schrage-Algorithmus an:Schrage-Algorithmus schrieb:
qundrseien definiert alsq := \left\lfloor \frac ma \right\rfloor, \; r := m \mod a \text{, sodass } m = aq + r.
Wenn
&0 \leq a(X\_n \mod q), r \left\lfloor \frac{X\_n}{q} \right\rfloor \leq m - 1\\ aX_n \mod m =&\begin{cases} a(X\_n \mod q) - r \left\lfloor \frac{X\_n}{q} \right\rfloor, & \text{wenn der Term }\geq 0\text{ ist}\\ a(X\_n \mod q) - r \left\lfloor \frac{X\_n}{q} \right\rfloor + m, & \text{sonst} \end{cases}r < qist, dann gilt:Nun kann der lineare Kongruenzgenerator portabel ohne Speicherüberlauf implementiert werden.
2.2 Mersenne-Twister
Der Mersenne-Twister wurde 1997 von Makoto Matsumoto und Takuji Nishimura vorgestellt [MN98]. Er besitzt eine extrem lange Periode von
[e]lambda[/e] = 2[h]19937[/h] - 1, einer Mersenne-Primzahl, die dem Algorithmus seinen Namen gibt. Die Zufallszahlen sind 623-dimensional gleichverteilt, d. h. teilt man die Zahlenreihe inn-Tupel mitn [e]le[/e] 623, so sind diese gleichverteilt imn-dimensionalen Raum (im Gegensatz zum linearen Kongruenzgenerator, der ohne erheblichen Aufwand nur bis zu fünfdimensional gleichverteilt ist). Außerdem sind alle Bits für sich gesehen gleichverteilt. Die Schnelligkeit des Algorithmus ist auf älteren Rechnern eingeschränkt, da er 624 Datenwörter Speicher benötigt, d. h. auf einer 32-Bit-Architektur624 * 32 [e]asymp[/e] 2,44 kB, und somit manchmal nicht vollständig in den besonders schnellen Cache geladen wird.Den Algorithmus in seiner ersten veröffentlichten Version (er wurde im Laufe der Jahre noch erheblich verbessert) findet man bei [MN98, S. 15].
3 Wahrscheinlichkeitsverteilungen
Oftmals braucht man für eine bestimmte Anwendung eine andere Wahrscheinlichkeitsverteilung als die Gleichverteilung. Deshalb sind verschiedene Algorithmen entwickelt worden, um eine solche Transformation zu implementieren. Dieses Kapitel widmet sich den Grundideen dreier solcher Transformationen.
Anmerkung: Da die folgenden Algorithmen eine gleichverteilte Zufallsvariable im Intervall
[0;1[erwarten, werden die vom linearen Kongruenzgenerator erzeugten Zufallszahlen auf diesen Bereich abgebildet:Eine wichtige Funktion in diesem Kapitel wird die (kumulative) Verteilungsfunktion sein. Sie summiert die Wahrscheinlichkeiten bis zu einem bestimmten Wert
F(x) &= P(X \leq x)\\ \int \limits_{-\infty}^{+\infty}F(x) dx &= 1\\ F(x\_1) \leq F(x\_2), &\, \text{wenn } x\_1 \leq x\_2\\ F(-\infty) = 0, &\,\, F(+\infty) = 1x, sodass gilt:3.1 Inversionsmethode
Für die Umwandlung von der Gleichverteilung zu einer anderen Verteilung braucht man eine Funktion, welche die Wahrscheinlichkeit, einen bestimmten Wert zu treffen, gewichtet. Man betrachte den Graphen einer streng monoton steigenden, stetigen Verteilungsfunktion, beispielsweise den der Verteilungsfunktion einer Exponentialverteilung
Bereiche, in denen die Steigung
dy/dxbesonders groß ist, sollen auch besonders von der Umwandlungsfunktion, welche die Gleichverteilung in eine Exponentialverteilung umwandelt, gewichtet werden. Die Umkehrfunktiondx/dyder Verteilungsfunktion tut genau dies. Somit lässt sich mittels jener aus einer gleichverteilten ZufallsvariablenUeine ZufallsvariableXmit der Dichtef(x)gewinnen:Eine Zufallszahl mit Exponentialverteilung erhält man also über
Da
Ugleichverteilt zwischen 0 und 1 ist, kann man das Argument des natürlichen Logarithmus sogar noch vereinfachen:Kann die Umkehrfunktion nicht direkt gebildet werden (beispielsweise weil die Verteilungsfunktion nicht injektiv ist), verschafft die Quantilfunktion Abhilfe (siehe http://de.wikipedia.org/wiki/Quantilfunktion):
F^{-1}(p) := \inf \left\{x \in \mathds R : F(x) \geq p\right\}
Die Inversionsmethode ist prinzipiell universell einsetzbar, wenn die Dichtefunktion integrierbar und die resultierende Verteilungsfunktion invertierbar ist (was bei der Normalverteilung beispielsweise nicht der Fall ist). Es scheitert jedoch meist an der nur schwer möglichen oder langsamen Berechnung von
F[h]-1[/h](x). Aus diesem Grund wurden für viele gängige Wahrscheinlichkeitsverteilungen andere Algorithmen entwickelt.Daneben gibt es die Möglichkeit, Wahrscheinlichkeitsverteilungen anzunähern. So ist
eine im Intervall
[0,0012499; 0,9986501]um mindestens eine Nachkommastelle genaue Approximation für die inverse Verteilungsfunktion der Standardnormalverteilung [Wur02, S. 42]. Durchgelangt man zur allgemeinen Normalverteilung.
3.2 Polarmethode
Die Polarmethode dient der Erzeugung standardnormalverteilter Zufallszahlen. Man benötigt dazu zwei gleichverteilte Zufallsvariablen zwischen -1 und 1:
V\_1 = 2U\_1 - 1, &\, V\_2 = 2U\_2 - 1\\ S &= V\_1^2 + V\_2^2Ist
S [e]le[/e] 1undS [e]ne[/e] 0(dafür muss der obige Schritt im Schnitt4/[e]pi[/e]-mal ausgeführt werden), liegt der Punkt, der durch die Koordinaten(V[t]1[/t]|V[t]2[/t])beschrieben wird, im Einheitskreis. Auf Grund dieser geometrischen Betrachtung ist der Name "Polarmethode" entstanden, da nun mit Hilfe der Polarkoordinaten des Punktes alle trigonometrischen Funktionen eliminiert werden können als Verbesserung der Box-Müller-Methode.Berechnet man nun
so sind
X[t]1[/t]undX[t]2[/t]normalverteilt [Knu97, S. 123].3.3 Verwerfungsmethode
Bereits im letzten Abschnitt wurde ein Beispiel der Verwerfungsmethode vorgestellt, jedoch ohne es beim Namen zu nennen: Ist der quadrierte Radius größer als 1, so werden die beiden gleichverteilten Zufallsvariablen abgelehnt, da der durch sie beschriebene Punkt nicht im Einheitskreis liegt.
Die Verwerfungsmethode, die 1951 von John von Neumann vorgeschlagen wurde [vN51, S. 36-38] und einen praktikablen Weg zur Erzeugung von Zufallsvariablen mit einer komplizierten Verteilungsfunktion darstellt, verallgemeinert diesen Schritt.
F(x)sei die Verteilungsfunktion der Wahrscheinlichkeitsverteilung, die erreicht werden soll,f(x)die Dichtefunktion. Man wähle nun eine (einfache) VerteilungsfunktionG(x)mit Dichtefunktiong(x)und bekannter InverseG^{-1}(x), sowie eine konstante reelle Zahlc, sodassf(x) \leq c \cdot g(x) \quad (\forall x \in \mathds R)
gilt.
Die Grundüberlegung der Verwerfungsmethode ist folgende: Um eine
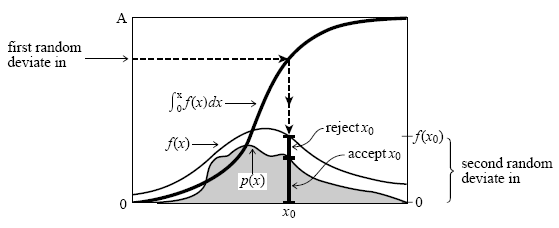
G-verteilte Zufallsvariable zu erhalten, kann man die Inversionsmethode anwenden (s. Abschnitt 3.1), d. h.G[h]-1[/h](U[t]1[/t])besitzt die Dichteg(x). Betrachtet man diesen Funktionswert als Abszisse ("x-Koordinate") eines zweidimensionalen Punktes mit der dazugehörigen Ordinate ("y-Koordinate")c * U[t]2[/t] * g(G[h]-1[/h](U[t]1[/t])), so sind die resultierenden Punkte gleichverteilt unter dem Graphen vonc * g(x). Verwirft man nun alle Punkte, die oberhalb des Graphen vonf(x)liegen, so unterliegt die Abszisse derselben Argumentation folgend derF-Verteilung. Demnach erhält man letztere, indem man so lange Tupel(U[t]1[/t], U[t]2[/t])aus gleichverteilten Zahlen erstellt, bisgilt. Abbildung 1 visualisiert diesen Algorithmus (hierbei ist zu beachten, dass die umhüllende Funktion in diesem Schaubild
f(x)und die zu erreichende Funktionp(x)heißt).
Veranschaulichung der Verwerfungsmethode [PTV93, S. 291]Da die resultierenden Punkte unterhalb des Graphen von
c * g(x)gleichverteilt sind und die Flächen unter den Graphenf(x)undc * g(x)gleich1respektivecsind, muss man im SchnittcTupel wählen, bis man einen geeigneten Punkt gefunden hat. Deshalb sollte mang(x)so wählen, dass der Graph dieser Funktion ähnlich verläuft wie der Graph vonf(x), sodass die Konstantecklein gewählt werden kann.Ist eine Kombination aus kleiner Konstante
cund schnell berechenbarer QuantilfunktionG[h]-1[/h](x)gefunden, stellt die Verwerfungsmethode eine effiziente Quelle für Zufallsvariablen, die nicht gleichverteilt sind, dar. Allerdings bietet sie keine Sicherheit, wenn Zufallszahlen zuverlässig sehr schnell benötigt werden, da es vorkommen kann, dass mehrere Tupel verworfen werden, ehe der Algorithmus terminiert.4 Statistische Tests
Um die Güte eines Zufallsgenerators zu prüfen, sind unzählige Tests entwickelt worden. Sie liefern ein objektives Maß für einen bestimmten Teilaspekt, unter dem Generatoren verglichen werden sollen. Zwar kann man nicht garantieren, dass ein Algorithmus, der eine bestimmte Zahl an Tests bestanden hat, automatisch beim nächsten nicht schlecht abschneidet, doch es gibt mittlerweile breit gefächert die verschiedensten Ansätze, um die Wahrscheinlichkeit dafür zu verringern.
Neben den theoretischen Tests, die die Funktionsvorschrift eines Generators mathematisch untersuchen und daraus Schlüsse ziehen, gibt es die empirischen Tests, welche vom Generator erzeugte Folgen statistisch auswerten. Aus der Vielzahl an Tests aus der letztgenannten Gruppe werden zwei wichtige in diesem Kapitel behandelt.
4.1 [c][e]chi[/e][h]2[/h][/c]-Test
Der
[e]chi[/e][h]2[/h]-Test wurde im Jahre 1900 von Karl Pearson eingeführt [Pea00, S. 157 - 175] und zählt zu den wohl bekanntesten Tests.Man nehme eine diskrete Wahrscheinlichkeitsverteilung mit
\chi^2 &= \sum\limits_{s = 1}^k \frac{\left( Y\_s - np\_s\right)^2}{np_s}\\ &= \frac 1n \sum\limits_{s = 1}^k \left(\frac{Y\_s^2}{p\_s}\right) - nkKategorien oder eine kontinuierliche, die inkKategorien, die in sich nicht mehr unterschieden werden, unterteilt wird. Nun macht mannvoneinander unabhängige Beobachtungen und zählt die Anzahl der TrefferY[t]s[/t]in jeder Kategories. Die erwartete Trefferanzahl ist offensichtlichnp[t]s[/t]. Die Differenz zwischen diesem Erwartungswert und dem empirischen Wert wird quadriert und anschließend gewichtet, d. h. je wahrscheinlicher ein Treffer in einer Kategorie ist, desto weniger zählt die quadrierte Differenz, da diese wahrscheinlich höher ausfällt als eine quadrierte Differenz in einer unwahrscheinlichen Kategorie (20 Treffer bei einem Erwartungswert von 25 sind wahrscheinlicher als sechs Treffer bei einem erwarteten). Die gewichteten quadrierten Differenzen werden schließlich addiert, sodass sich folgende Formel ergibt:Nun kann man in einer Tabelle der
[e]chi[/e][h]2[/h]-Verteilung nachschlagen oder direkt mit der Verteilung ausrechnen, wie wahrscheinlich eine solche Abweichung[e]chi[/e][h]2[/h]ist. Dazu benötigt man nur noch den Freiheitsgrad[e]nu[/e], d. h. die Anzahl der voneinander unabhängigen Parameter. Dieser entspricht[e]nu[/e] = k - 1(hat man alle ParameterY[t]1[/t]bisY[t]k - 1[/t], lässt sichY[t]k[/t]berechnen).Eine Beispielrechnung: Wirft man fünf nicht unterscheidbare Münzen gleichzeitig, erhält man nach 1024 Versuchsdurchführungen möglicherweise folgende Ergebnisse:
\chi^2 &= \frac{9}{32} + \frac{49}{160} + \frac{5}{16} + \frac{121}{320} + \frac{1}{10} + \frac{1}{32}\\ &= 1 \frac{131}{320}.
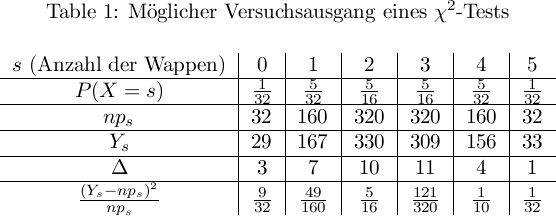
Der Wert[e]chi[/e][h]2[/h]wäre nach dieserSchaut man diesen Wert bei
[e]nu[/e] = 5Freiheitsgraden in der Tabelle nach, sieht man, dass der Wert geringer ist als der Wert 1,61 bei der 90%-Marke. Somit liegt die Wahrscheinlichkeit für ein solch geringes[e]chi[/e][h]2[/h]bei unter 10%, sodass der Verdacht entsteht, dass es beim Experiment nicht mit rechten Dingen zuging (natürlich ist es schwer, in der Realität Münzen zu gut zu werfen, aber bei Zufallsgeneratoren ist dies durchaus möglich).Zwar ist die Tabelle nur von
[e]nu[/e]abhängig und nicht vonp[t]s[/t]undn. Dennoch ist die Wahl von letzterem wichtig, denn die[e]chi[/e][h]2[/h]-Verteilung und damit auch die Tabelle ist nur ein Näherungswert für großen. Als Faustregel sollte jede erwartete Trefferanzahl mindestensnp[t]s[/t] > 5sein. Der Grund für diese Ungenauigkeit liegt in der Diskretheit von[e]chi[/e][h]2[/h], da die empirische Trefferanzahl diskret ist. Somit kann die Tabelle recht deutlich von den genauen Werten abweichen, weshalb es manchmal sinnvoll ist, auf Grund des gegebenen Experiments eine genauere Tabelle zu erstellen.Ein großes
nsorgt auf Grund des Gesetzes der großen Zahlen dafür, dass globale Nichtzufälligkeit leichter entdeckt wird, doch verschleiert lokale Nichtzufälligkeit: Wenn die Wahrscheinlichkeit für eine Kategorie z. B. bei einer Hälfte der Versuchsdurchführungen konstant zu niedrig und bei der anderen Hälfte konstant zu hoch ist, wird man dies mit einem[e]chi[/e][h]2[/h]-Test mit großemnnur schwer feststellen können. Somit sollte ein Kompromiss für die Größe von gefunden oder der Test mit verschiedenen Werten fürnwiederholt werden.4.2 Kolmogorow-Smirnow-Test
Im Jahre 1933 veröffentlichte A. N. Kolmogorow die erste Version eines statistischen Tests, der später nach ihm benannt werden sollte. N. V. Smirnow untersuchte sechs Jahre später verschiedene Modifikationen an diesem Test, wodurch die heutige Form des Kolmogorow-Smirnow-Tests (im Folgenden KS-Test genannt) entstand. Die Grundidee ist folgende:
F(x)sei eine stetige VerteilungsfunktionAnmerkung: Die Wahl einer diskreten Verteilungsfunktion ist ebenfalls möglich, doch dann wird der Test weniger trennscharf, d. h. die Nullhypothese wird seltener verworfen.
Auf Grund einer Versuchsreihe mit
nverschiedenen ZahlenX[t]1[/t], X[t]2[/t], ..., X[t]n[/t]bildet man die empirische VerteilungsfunktionEs ist ersichlich, dass
0 [e]le[/e] F(x), F[t]n[/t](x) [e]le[/e] 1gilt.Der KS-Test ermittelt nun die maximale Abweichung der empirischen Verteilungsfunktion von der gewünschten Verteilungsfunktion in beide Richtungen, d. h.
K\_n^{+} &= \sqrt{n} \sup \limits\_{-\infty < x < +\infty} \left(F_n(x) - F(x)\right),\\ K\_n^{-} &= \sqrt{n} \sup \limits\_{-\infty < x < +\infty} \left(F(x) - F_n(x)\right).Die Multiplikation mit ist sinnvoll, da
F[t]n[/t](x)bei festem, aber beliebigenxantiproportional zu ist.K[t]n[/t][h]+[/h]undK[t]n[/t][h]-[/h]können nun wieder in einer Tabelle nachgeschlagen werden.Verlauf von
K[t]n[/t]und der empirischen Verteilungsfunktion im Vergleich zur Verteilungsfunktion der Normalverteilung:
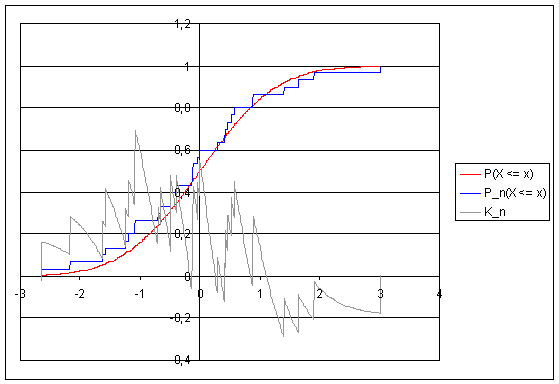
Um den Test visuell zu veranschaulichen, habe ich oben stehende Abbildung mit folgenden Eigenschaften erstellt: Der lineare Kongruenzgenerator hat die Parameter
X[t]0[/t] = 123459876, a = 7[h]5[/h] = 16807, c = 0undm = 2[h]31[/h] - 1 = 2147483647, wie sie von Park und Miller im Jahre 1988 als "minimaler Standard" vorgeschlagen wurden [PM88, S. 1192 - 1201]. Mittels der Polarmethode wird die Gleichverteilung in eine Normalverteilung umgewandelt.Man erkennt, dass die empirischen Werte im negativen Bereich zu klein, d. h.
F[t]n[/t](x)zu groß ist. Diese Abweichung ist deutlich größer als die gegenläufige Abweichung im positiven Bereich der Abszisse. Dies spiegelt sich auch in den Ergebnissen des KS-Tests wider:K[t]n[/t][h]+[/h] = 0,694beix = -1,081
K[t]n[/t][h]-[/h] = 0,288beix = 1,405Die Wahrscheinlichkeit für ein solch kleines
K[t]n[/t][h]-[/h]liegt zwischen 5% und 25%, jene für ein solch großesK[t]n[/t][h]+[/h]zwischen 25% und 50%. Dies sind akzeptable Werte, v. a. wenn man bedenkt, dass zwei aufeinanderfolgende Zufallszahlen des linearen Kongruenzgenerators nicht komplett unabhängig voneinander sind.Wie schon beim
[e]chi[/e][h]2[/h]-Test gilt bei diesem Test wieder ein besonderes Augenmerk der Wahl des Parametersn. Zwar ist der KS-Test auch schon für ungewöhnlich kleine Werte vonnausreichend gut, aber auch hier gilt, dass die NullhypotheseF[t]n[/t](x) = F(x)besser mit einem großennverworfen werden kann. Auch wird wieder lokale Nichtzufälligkeit mit kleinemnbesser erkannt.Beide Eigenschaften kann man verbinden, indem man den Test mehrmals hintereinander mit einem relativ großen
ndurchführt und auf die resultierenden WerteK[t]n[/t][h]+[/h](1), K[t]n[/t][h]+[/h](2), ...wiederum einen KS-Test anwendet. Die Verteilungsfunktion fürK[t]n[/t][h]+[/h]wird dabei für großendurchangenähert [Knu97, S. 50 - 52].
Auf diese Weise kann man den KS-Test ebenfalls mit dem
[e]chi[/e][h]2[/h]-Test kombinieren, sodass beide Tests gemeinsam eine erste Einschätzung für die Qualität eines Algorithmus liefern.5 Fazit
Diese Arbeit gibt einen kurzen Einblick in die Welt der Pseudozufallszahlen. Sie vermittelt grundsätzliche Überlegungen zur Erzeugung pseudozufälliger Zahlen mittels des linearen Kongruenzgenerators und stellt einige Algorithmen zur Erzeugung verschiedener Wahrscheinlichkeitsverteilungen sowie Tests, die Aussagen über die Güte eines Generators bzw. Algorithmus treffen, vor.
Bei der Erarbeitung des Themenkomplexes stellte ich fest, dass in Programmcode oftmals nicht auf die Eigenschaften von Pseudozufallszahlen eingegangen wird. So ist folgendes Konstrukt für eine gleichverteilte, ganzzahlige Zufallszahl zwischen 0 und 999 weit verbreitet (Pseudocode):
var x = rand() mod 1000Es ist offensichtlich, dass diese Art der Abbildung der Funktionswerte von
rand()auf das gewünschte Intervall die Gleichverteilung umso mehr stört, je größer das Modul gegenüber dem Maximalwert vonrand()ist. Desweiteren tritt hier, wenn bei der Erzeugungsmethode nicht Sorge getragen wurde, wieder die verkürzte Periode der niederwertigen Bits in Erscheinung.Doch auch Programmierer von Zufallsgeneratoren neigen zu mathematischen Fehlgriffen mit dem Ziel der Verbesserung ihrer Generatoren. So tauschte die
rand()-Implementierung eines bekannten C-Compilers die obere und untere Hälfte der erzeugten Zahlen, worunter die Zufälligkeit der erzeugten Folge massiv litt [PTV93, S. 277]. Angesichts des jungen Alters dieses Fachgebiets (auch weil es Computer noch nicht lange als Massenprodukt gibt) kann man allerdings hoffen, dass diese Mängel größtenteils in kurzer Zeit behoben sein werden.So viel zur Theorie hinter dem berüchtigten rand(). Wie man den Zufall am besten in sein C++-Programm integriert, zeigt der interessante Artikel "Zufälle gibt's!" von Marc++us.
6 Literatur
[Knu97] KNUTH, DONALD E.: The Art of Computer Programming, Volume 2: Seminumerical
Algorithms. Addison-Wesley, Reading, Massachusetts, Third Edition ,
1997.[Leh51] LEHMER, DERRICK H.: Proc. Second Sympos. on Large-Scale Digital Calculating
Machinery. Cambridge, Mass.: Harvard University Press, 1951.[MN98] MATSUMOTO, M. T. NISHIMURA: Mersenne Twister: A 623-dimensionally equidistributed
uniform pseudorandom number generator. ACM Trans. on Modeling
and Computer Simulations, 1998.[Pea00] PEARSON, KARL: Random Sampling. Philosophical Magazine, 50, 1900.
[PM88] PARK, STEPHEN. K. KEITH W. MILLER. Communications of the ACM, 32,
1988.[PTV93] PRESS, WILLIAM H., SAUL A. TEUKOLSKY WILLIAM T. VETTERLING: Numerical
Recipes in C: The Art of Scientific Computing. Cambridge University Press,
1993.[Sch79] SCHRAGE, LINUS E.: A More Portable Fortran Random Number Generator.
ACM Transactions on Mathematical Software, 5, 1979.[vN51] NEUMANN, JOHN VON: Various techniques used in connection with random
digits. Monte Carlo methods. Nat. Bureau Standards, 12. 1951.[Wur02] WURST, ULRICH: Realistische Lasteinspeisung in Emulationsszenarien. ,
Institut für Parallele und Verteilte Systeme, Universität Stuttgart, 2002.
(http://elib.uni-stuttgart.de/opus/volltexte/2003/1311/pdf/STUD-1856.pdf).
-
vielen Dank! Super Artikel!
-
Michael E. schrieb:
3 Wahrscheinlichkeitsverteilungen
...
Eine wichtige Funktion in diesem Kapitel wird die (kumulative) Verteilungsfunktion sein. Sie summiert die Wahrscheinlichkeiten bis zu einem bestimmten Wert x, sodass gilt:
...
\int \limits_{-\infty}^{+\infty}F(x) dx &= 1\\Das gilt für die Dichtefunktion, nicht für die Verteilungsfunktion.

-
Da hast du recht. Danke für den Hinweis. Ich werde es mitsamt der mittlerweile verunstalteten Typographie in den nächsten Tagen ausbessern.
-
Aha und wann?
-
Bei der Erarbeitung des Themenkomplexes stellte ich fest, dass in Programmcode oftmals nicht auf die Eigenschaften von Pseudozufallszahlen eingegangen wird. So ist folgendes Konstrukt für eine gleichverteilte, ganzzahlige Zufallszahl zwischen 0 und 999 weit verbreitet (Pseudocode):
Code:
var x = rand() mod 1000Es ist offensichtlich, dass diese Art der Abbildung der Funktionswerte von rand() auf das gewünschte Intervall die Gleichverteilung umso mehr stört, je größer das Modul gegenüber dem Maximalwert von rand() ist. Desweiteren tritt hier, wenn bei der Erzeugungsmethode nicht Sorge getragen wurde, wieder die verkürzte Periode der niederwertigen Bits in Erscheinung.
Doch auch Programmierer von Zufallsgeneratoren neigen zu mathematischen Fehlgriffen mit dem Ziel der Verbesserung ihrer Generatoren. So tauschte die rand()-Implementierung eines bekannten C-Compilers die obere und untere Hälfte der erzeugten Zahlen, worunter die Zufälligkeit der erzeugten Folge massiv litt [PTV93, S. 277]. Angesichts des jungen Alters dieses Fachgebiets (auch weil es Computer noch nicht lange als Massenprodukt gibt) kann man allerdings hoffen, dass diese Mängel größtenteils in kurzer Zeit behoben sein werden.