[A] Grafik-Programmierung - Nötige Mathematik

Walnut_Burl

Einführung

Grafische Programmierung wird in der heutigen Zeit immer wichtiger. Ob man sie für Videospiele, physikalische Simulationen oder auch für medizinische Anwendungen gebraucht. Sie ist kaum noch wegzudenken.
Da sehr viele angehende Programmierer sich mit eben dieser beschäftigen wollen, müssen sie auch die nötige Mathematik dafür kennen.

In diesem Artikel werde ich auf die Programmierung mit DirectX 10 eingehen (wobei die gelernten mathematischen Formeln auch für jede andere Grafik-API zutreffen). Zwei zentrale Aspekte werden Matrizen und Vektoren, und natürlich auch deren Manipulationen darstellen.

Inhaltsverzeichnis

**

1. Vektoren
1.1 Allgemein
1.2 Vektormathematik
1.3 DirectX Funktionen zur Berechnung von Vektoren
1.4 Zusammenfassung
2. Punkte
2.1 Allgemein
2.2 Ähnlichkeiten zwischen Vektoren und Punkten
2.3 Zusammenfassung
3. Matrizen
3.1 Allgemein
3.2 Matrixmathematik
3.3 Relevante Matrixtypen
3.4 DirectX Funktionen zur Berechnung von Matrizen
3.5 Zusammenfassung
4. Aufgaben
4.1 Vektoren/Punkte
4.2 Matrizen
Lösungen

**

1. Vektoren

1.1 Allgemein

Vektoren repräsentieren Pfeile mit einer bestimmten Länge in Koordinatensystemen, weshalb sie das grundlegenste Mittel in der Programmierung mit einer Grafik-API sind. Mit ihnen kann man Dreiecke zeichnen, die dazu gebraucht werden um Gegenstände in der virtuellen Welt zu zeigen. Als Beispiel kann man sich hier einen Würfel mit 6 gleichgroßen Seiten anschauen. Um diesen Würfel mit Vektoren anschaulich zu machen, würde man an jedem Eckpunkt einen Punkt in einem Koordinatensystem legen, und diese dann via Dreiecken miteinander verbinden. Dies hört sich jetzt noch schwieriger an als es im Endeffekt ist (wobei in diesem Artikel nicht auf das Zeichnen von Objekten, sondern nur auf die nötige Mathematik dafür eingegangen).
Außerdem gebraucht man Vektoren um Kräfte, Richtungen, Verschiebungen und Geschwindigkeiten darzustellen.
Ein Vektor sieht wird folgendermaßen mathematisch dargestellt:

[c]v = (v[t]x[/t], v[t]y[/t], v[t]z[/t])    //ein 3D Vektor[/c]

Nun eine kleine Erläuterung des vorher geschriebenen. v ist hier der Name des Vektors. Diesem Vektor v werden die Koordinaten v_x, v_y, und v_z zugewiesen. Möchte man unserem Vektor v nun Zahlen zuweisen, ginge diese so:

[c]v = (1, 2, 3)    //Vektor mit zugewiesenen Koordinaten[/c]

Da es einfacher ist mit 2D-Vektoren zu arbeiten, werden ab sofort diese gebraucht (bis wir zu den DirectX Funktionen kommen).

Wikipedia hat eine nette Begriffserklärung für Vektoren, die ich ihnen gerne durch ein Zitat näher bringen würde:

Wikipedia schrieb:

Ein Vektor (lat.: vector = „Träger“, „jemand, der zieht/befördert“; zu lat.: vehere = „[etwas/jemanden] fahren/transportieren“) ist in der Mathematik ein Element eines Vektorraums. Das bedeutet unter anderem, dass sich beliebige zwei Vektoren durch Addition zu einem dritten Vektor des gleichen Vektorraums verknüpfen lassen. Eine Multiplikation zwischen Vektoren kann definiert sein, muss aber nicht.

http://de.wikipedia.org/wiki/Vektor

1.2 Vektormathematik

Da wir jetzt wissen wie man einen Vektor im Allgemeinen darstellt, widmen wir uns nun deren Mathematik. Die einfachsten Vektor Operationen sind folgende:

Zwei Vektoren sind gleich, wenn die Komponenten beider Vektoren gleich sind. Das heißt, v ist gleich u , wenn

[c](v[t]x[/t] = u[t]x[/t], v[t]y[/t] = u[t]y[/t])[/c]

Bei einer Addition von Vektoren werden alle zugehörigen Komponenten addiert. Wenn man einen Vektor v

[c]v = (1, 2)[/c]

mit einem neuen Vektor u

[c]u = (4, -2)[/c]

addieren, so würde man wie folgt vorgehen:

v + u = (1, 2) + (4, -2) = (5, 0)

In einem Koordinatensystem sähe eine solche Addition folgendermaßen aus:

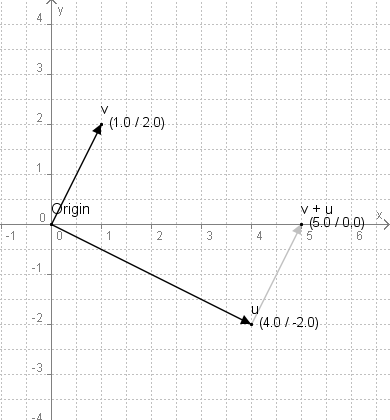
Die beiden Vektoren v und u ergeben addiert den neuen Vektor v + u . Verschiebt man den Vektor v , so dass sein "Schwanz" (das hintere Ende), den "Kopf" (Spitze) des Vektors u berührt, und weiterhin parallel zu dem Originalvektor v bleibt, so liegt der "Kopf" des neuen Vektors v + u , an dem Kopf des verschobenen Vektors v' .

Bei einer Subtraktion von Vektoren werden alle zugehörigen Komponenten subtrahiert. Dies sieht folgendermaßen aus:

v = (1, 2)
u = (4, -2)
v - u = (1, 2) - (4, -2) = (-3, 4)    //wichtig hier [-] * [-] ergibt [+]  :cool:

Hier natürlich auch wieder ein Beispiel in einem Koordinatensystem:

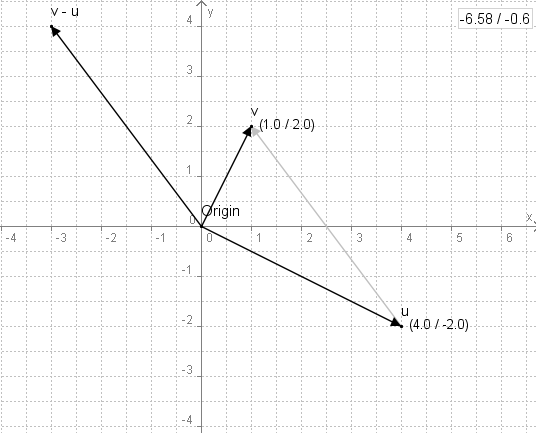
Die beiden Vektoren v und u ergeben subtrahiert den neuen Vektor v - u . Wie man sieht ist die Strecke von u zu v die Länge des Vektors v - u , gemessen ab dem Punkt Origin .

Zusätzlich zu der Addition und Subtraktion von Vektoren gibt es noch die Multiplikation eines Vektors mit einer reellen Zahl. Hierbei multipliziert man jede der Komponenten einzeln mit der reellen Zahl(auch oft Skalar genannt). Ein einfaches Beispiel hierzu:

s = -2
v = (1, 2)
sv = (1*(-2), 2*(-2)) = (-2, -4)

Zur Veranschaulichung ein weiteres Koordinatensystembeispiel:

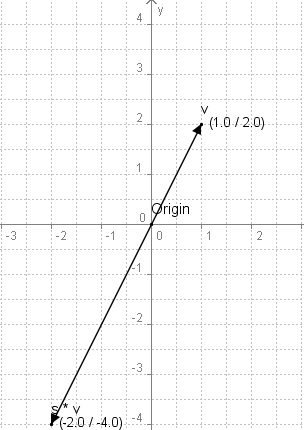
Diese Abbildung zeigt einen Vektor, multipliziert mit einer reellen Zahl (-2). Wie man sieht wurde die Länge des Vektors verdoppelt, und die Richtung des Vektors umgekehrt. Daraus kann man schließen, dass, wenn man einen Vektor negiert, die Richtung in die der Vektor zeigt sich umkehrt. Außerdem wird klar, dass man mit einer Multiplikation mit einer reellen Zahl die Länge des Vektors verändern kann.

Um weiter folgen zu können muss hier nun ein kleiner Einschnitt gemacht werden. Es gibt 2 Sonderarten von mathematischen Formeln für Vektoren. Erstens kann man den Betrag (Länge) eines Vektors ausrechnen, und zweitens kann man einen Vektor normieren (vereinheitlichen oder auf die Länge 1 bringen).
Die Länge eines Vektors kann man herausfinden, indem man die quadrierten Komponenten addiert und dann die Wurzel zieht. In einem konkreten Beispiel sähe das so aus:

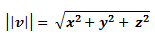
Wie man sieht, wird der Betrag eines Vektors, mit 2 Betragstrichen gekennzeichnet. Grundsätzlich gilt also folgende Syntax:

||[i]name[/i]||

Wenn man den Betrag eines Vektors ausgerechnet hat, dann erhält man die Länge des Vektors von seinem "Schwanz" bis zu seinem "Kopf". Nun noch ein Beispiel, mit konkreten Zahlen (hier gebrauchen wir wieder nur einen 2D Vektor, wobei das Beispiel auch problemlos auf 3D, 4D und so weiter anzuwenden ist.

v = (1, 2)
[pic]GraphischeProgrammierung-NötigeMathematik/Lengthvectorex.png[/pic]
||v|| [e]asymp[/e] 2,24

Hier natürlich auch wieder ein kleines Beispiel:

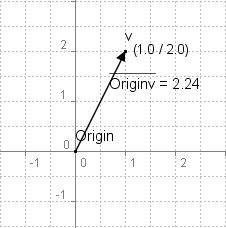
Die Länge des Vektors v .

Da der Leser, um einen Vektor zu normieren, erst die Länge eines Vektors herausfinden muss, kommen die Einheitsvektoren erst jetzt an die Reihe. Ein Einheitsvektor hat im Endeffekt die Länge 1! Der Normvektor, wird, wie der interessierte Leser später herausfinden wird, für viele wichtige Funktionen in DirectX gebraucht. Ich beschränke mich jetzt auf die mathematische Formel um den Normvektor aus jeden erdenklichen Vektor zu finden. Die Formel lautet wie folgt:

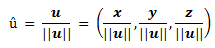
Auch hier ein Beispiel mit konkreten Zahlen:

u = (4, -2)
[pic]GraphischeProgrammierung-NötigeMathematik/Einheitsvektorex.png[/pic]

In einem Koordinatensystem:

Wie man sieht hat der Vektor û jetzt eine Länge von 1 und ist somit ein Einheitsvektor.

Nun widme ich mich den etwas spezielleren mathematischen Formeln. Als erstes wird das Skalarprodukt behandelt. Bei eben diesem Produkt, erhalten wir keinen Vektor, sondern eine reelle Zahl. Die Syntax eines Skalarprodukts sieht folgendermaßen aus:

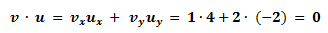
Das Skalarprodukt hat keine wirkliche geometrische Bedeutung, doch in der folgenden Formel kann man den Zusammenhang erkennen.

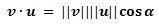
Durch diese Formel kann man den Winkel [e]alpha[/e] herausfinden.
Wobei der Winkel [e]alpha[/e] der folgende ist:

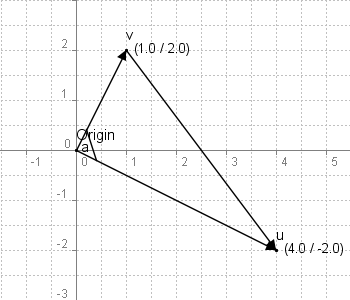
Der Winkel α liegt zwischen den beiden Vektoren, v und u .
Die zweite spezielle mathematische Formel ist das sogenannte Kreuzprodukt. Sie lässt sich nur im dreidimensionalen Bereich ausführen, und ist ein wenig schwerer zu beschreiben und zu verstehen als die übrigen Operationen. Eine gelungene Grafik, die das Kreuzprodukt darstellt kann man sich hier anschauen:
http://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Crossproduct.png/400px-Crossproduct.png

Ich werde nun nur auf die Syntax der mathematischen Operation eingehen, die wie folgt lautet:

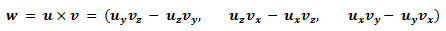
Auch hier natürlich ein kleines Beispiel welches die Syntax etwas veranschaulicht:

v = (1, 2, 3)
u = (4, -2, 3)
[pic]GraphischeProgrammierung-NötigeMathematik/Crossex.png[/pic]

Die Syntax des Kreuzprodukts sieht auf den ersten Blick verwirrend und unmöglich zu lernen aus, aber irgendwann hat man es drauf. Außerdem wird die Arbeit durch DirectX Funktionen erheblich erleichtert.

Nun haben sie einen Überblick über alle wichtigen mathematischen Operationen die relevant für die Grafik-Programmierung sind.

1.3 DirectX Funktionen zur Berechnung von Vektoren

Alle DirectX Funktionen die wir in dieser kleinen DirectX-Einführung benutzen findet man in dem header d3dx10.h wieder. Wie man die DirectX SDK in den verwendeten Compiler einbettet, kann man sich im Internet auf zahlreichen Internetseiten anschaulich erklären lassen.

Nun fangen wir auch gleich an!
Vektoren werden in der DirectX-API mit diesen Funktionen dargestellt:

D3DXVECTOR2 v2    //2D Vektor
D3DXVECTOR3 v3    //3D Vektor
D3DXVECTOR4 v4    //4D Vektor

Um Vektoren in der Konsole anzeigen zu lassen, müssen wir den operator<< überladen.

ostream& operator<<(ostream& os, D3DXVECTOR3 v)
{
	os << "( " << v.x << ", " << v.y << ", " << v.z << " )";
	return os;
}

DirectX hält außerdem noch folgende Funktionen zur Manipulation von Vektoren bereit:

FLOAT D3DXVec3Length(         //gibt ||v|| zurück
    CONST D3DXVECTOR3 *pV);   //Eingabe von v

FLOAT D3DXVec3LengthSq(       //gibt ||v||[h]2[/h] zurück
    CONST D3DXVECTOR3 *pV);   //Eingabe von v

FLOAT D3DXVec3Dot(            //gibt v[t]1[/t] . v[t]2[/t] zurück
    CONST D3DXVECTOR3 *pV1,   //Eingabe von v[t]1[/t]
    CONST D3DXVECTOR3 *pV2);  //Eingabe von v[t]2[/t]

D3DXVECTOR3 *D3DXVec3Cross(   
    D3DXVECTOR3 *pOUT,        //gibt v[t]1[/t] x v[t]2[/t] zurück
    CONST D3DXVECTOR3 *pV1,   //Eingabe von v[t]1[/t]
    CONST D3DXVECTOR3 *pV2);  //Eingabe von v[t]2[/t]

D3DXVECTOR3 *WINAPI D3DXVec3Normalize(
    D3DXVECTOR3 *pOut,        //gibt v / ||v|| zurück
    CONST D3DXVECTOR3 *pV);   //Eingabe von v

Um diese Funktionen dem Leser näher zu bringen, hier ein kleines ausführbares Beispiel:

//Veranschaulichung der DirectX 10 Funktionen relevant für Vektoren
#include<D3DX10.h>
#include<iostream>

using namespace std;

ostream& operator<<(ostream& os, D3DXVECTOR3 v)
{
	os << "( " << v.x << ", " << v.y << ", " << v.z << " )";
	return os;
}

int main()
{
	//Konstruktor D3DXVECTOR3(FLOAT x, FLOAT y, FLOAT z);
	D3DXVECTOR3 v(1.0f, 2.0f, 3.0f);

	//Konstruktor D3DXVECTOR3(CONST FLOAT*);
	float x[3] = {4.0f, -2.0f, 3.0f};
	D3DXVECTOR3 u(x);

	//Konstruktor D3DXVECTOR3();
	D3DXVECTOR3 a, b, c, d, e;

	//Addition
	a = v + u;
	//Subtraktion
	b = v - u;
	//Multipilkation mit einer reellen Zahl
	c = v * -2;
	//Länge von v (||v||)
	float Laenge = D3DXVec3Length(&v);
	//||v||²
	float LaengeQuadrat = D3DXVec3LengthSq(&v);
	//Normieren von v
	D3DXVec3Normalize(&d, &v);
	//Skalar-Multiplikation
	float Punkt = D3DXVec3Dot(&v, &u);
	//Kreuzprodukt
	D3DXVec3Cross(&e, &v, &u);

	//Ausgabe der Vektoren
	cout << "_____________________________" << endl;
	cout << "v                          = " << v << endl;
	cout << "u                          = " << u << endl;
	cout << "a = v + u                  = " << a << endl;
	cout << "b = v - u                  = " << b << endl;
	cout << "c = v * -2                 = " << c << endl;
	cout << "Laenge von v               = " << Laenge << endl;
	cout << "Laenge zum Quadrat von v   = " << LaengeQuadrat << endl;
	cout << "Normierter Vektor v        = " << d << endl;
	cout << "Skalar-Multiplikation      = " << Punkt << endl;
	cout << "Kreuzprodukt               = " << e << endl;
	cout << "_____________________________" << endl;

	cin.get();
	return 0;
}

Dies sind alle wichtigen Funktionen die man benötigt, um Vektoren wiederzugeben oder aber diese zu manipulieren.

1.4 Zusammenfassung

Vektoren spielen eine grundlegende Rolle in grafischen Anwendungen. Sie können Richtungen, Geschwindigkeiten, Kräfte und Verschiebungen representieren.
Mit Vektoren kann man verschiedene mathematische Operationen durchführen. Man kann Vektoren addieren, subtrahieren und sie mit einer reellen Zahl multiplizieren. Außerdem gibt es noch das Skalarprodukt und auch das Kreuzprodukt. Zusätzlich zu diesen Formeln, kann man noch die Länge eines Vektors herausfinden. Um einen Vektor auf die Länge 1 zu bringen, muss man ihn normieren.
DirectX hält genau für diese mathematischen Operationen einige Funktionen bereit. Die wichtigsten sind:

FLOAT D3DXVec3Length                     //gibt Länge eines Vektors zurück
FLOAT D3DXVec3LengthSq                   //gibt Potenzierte Länge zurück
FLOAT D3DXVec3Dot                        //gibt das Skalarprodukt von zwei Vektoren zurück
D3DXVECTOR3 *D3DXVec3Cross               //gibt das Kreuzprodukt von zwei Vektoren zurück
D3DXVECTOR3 *WINAPI D3DXVec3Normalize    //gibt normierten Vektor zurück

___________________________________________

2. Punkte

2.1 Allgemein

Anders als Vektoren, die Pfeile in Koordinatensystemen darstellen, repräsentieren Punkte einfache Positionen in einem Koordinatensystem. Dies wird zum Beispiel dafür gebraucht, die Position der virtuellen Kamera in unserer DirectX Applikation anzuzeigen.
Natürlich lässt sich mit Punkten auch rechnen, wobei hier einige Operationen partout keinen Sinn machen würden. Was wäre zum Beispiel die Addition zweier Punkte? Eine Subtraktion zweier Punkte hingegen ist vollkommen legitim, da hierbei ein neuer Vektor, der von Punkt 1 zu Punkt 2 reicht, entsteht. Nehmen wir an wir haben die Punkte v und u:

v = (1, 2)
u = (4, -2)

Die Subtraktion dieser beiden Punkte (v-u) sähe in einem Koordinatensystem wie folgt aus:

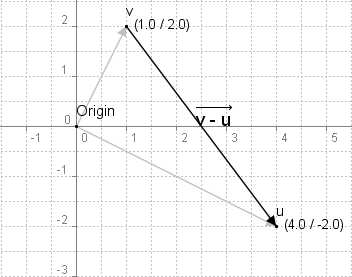
Der Vektor v-u reicht vom Punkte u bis zum Punkt v.

Zusätzlich zu der Subtraktion kann man auch einen Punkt mit einem Vektor addieren. Dies resultiert jedoch nicht in einem neuen Vektor sondern in einem neuen Punkt. Gegeben sind hier der Punkt p und der Vektor v .

p = (4, -2)
v = (1, 2)

In einem Koordinatensystem:

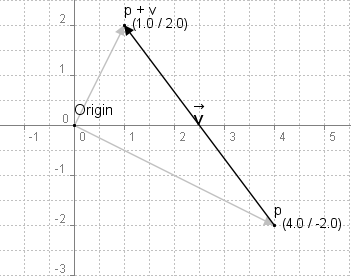
Durch eine Addition eines Vektors mit einem Punkt erhalten wir einen neuen Punkt am Ende des gegebenen Vektors.

Natürlich gibt es noch andere Operationen die man mit Punkten durchführen kann, doch entweder sind sie für uns nicht relevant oder aber sie sind mit denen zur Vektorbeeinflussung gleich.

Eine wichtige Sache gäbe es dennoch noch zu sagen. In DirectX gebraucht man meist den D3DXVECTOR4 Vektortyp, da man so zwischen Punkten und Vektoren unterscheiden kann. Um einen Punkt zu repräsentieren setzen wir die letzte Koordinate (x, y, z, w) zu 1. Bei einem Vektor zu 0. Das dies Sinn macht, möchte ich anhand zwei kleiner Beispiele zeigen.
Als erstes subtrahieren wir 2 Punkte miteinander. Von unserem Wissensstand aus, würden wir sagen, dass wir einen Vektor als Ergebnis bekommen. Nun können wir einen einfachen Test machen.

q - p = (p[t]x[/t], p[t]y[/t], p[t]z[/t], 1) + (p[t]x[/t], p[t]y[/t], p[t]z[/t], 1) = (p[t]x[/t]-p[t]x[/t], p[t]y[/t]-p[t]y[/t], p[t]z[/t]-p[t]z[/t], 0)

Wie man sieht resultiert diese Subtraktion in einem Vektor (x, y, z, 0).

Weiter nehmen wir an wir möchten einen Punkt mit einem Vektor addieren. Dies sähe dann wie folgt aus:

p + v = (q[t]x[/t], q[t]y[/t], q[t]z[/t], 1) + (v[t]x[/t], v[t]y[/t], v[t]z[/t], 0) = (q[t]x[/t]-v[t]x[/t], q[t]y[/t]-v[t]y[/t], q[t]z[/t]-v[t]z[/t], 1)

Auch hier sehen wir wieder das erwartete Ergebnis. Einen Punkt (x, y, z, 1).
Es ist keine Vorschrift, Vektoren und Punkte mit einer vierten Koordinate w zu versehen, doch bei einigen Operationen ist dies Pflicht, da sie sonst verfälschte Ergebnisse bringen.

1.2 Zusammenfassung

Punkte repräsentieren, anders als Vektoren keine Kräfte oder Ähnliches, sondern Positionen in Koordinatensystemen. Mit ihnen wird z.B. die Position der virtuellen Kamera angegeben.
Mit Punkten zu rechnen ist ebenfalls möglich, wobei einige Operationen undefiniert sind(Addition zweier Punkte).
Um zwischen Punkten und Vektoren besser unterscheiden zu können, benutzen wir 4D Vektoren und Punkte, wobei wir hier die 4. Koordinate für Punkte auf 1 und für Vektoren auf 0 setzen.

___________________________________________

3.Matrizen

3.1 Allgemein

Mit Matrizen kann man einfach Rotationen, Skalierungen, und Translationen darstellen. Wir werden uns nun einige wichtige Matrixtypen, sowie die Matrixmathematik anschauen.
Eine Matrix sieht folgendermaßen aus:

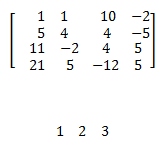
Oben: Eine 4(Reihen)x4(Zeilen) Matrix, mit reellen Zahlen ausgefüllt.
Unten: Eine 1x3 Matrix, mit reellen Zahlen ausgefüllt. Wie man sieht ist diese Matrix gleichzusetzen mit einem Vektor.

Um den Index der verschiedenen Zahlen herauszufinden, gehen wir folgendermaßen vor:

Die erste hochgestellte Zahl spezifiziert die Reihe. Die zweite die Spalte. Durch diese Technik kann man schnell herausfinden um welche Zahl der Matrix es sich explizit handelt.

3.2 Matrixmathematik

Für Matrizen gibt es eine ganze Reihe von mathematischen Operationen welche wir uns nun anschauen werden.

Man kann Matrizen miteinander addieren. Hierbei addiert man die Zahlen beider Matrizen des gleichen Index miteinander.

Ein Beispiel darf auch hier nicht fehlen.

Eine 3x3 Matrix addiert mit einer gleichgroßen Matrix ergibt wiederum eine 3 Zeilen mal 3 Spalten große Matrix.

Die zweite Arithmetische Operationen bezüglich Matrizen ist die Subtraktion von Matrizen. Die Subtraktion wird ähnlich der Addition bestritten. Das heißt, die Zahlen mit dem gleich Index werden voneinander subtrahiert. Als Beispiel:

Auch hier entsteht wieder eine 3x3 Matrix, da man eine 3x3 Matrix von einer weiteren 3x3 Matrix subtrahiert.
Die dritte Operation ist die Multiplikation zweier Matrizen. Man kann nur Matrizen multiplizieren wenn die Dimension der Reihen der einen Matrix der Dimension der Spalten der zweiten Matrix entspricht. Das heißt eine M x N Matrix multipliziert mit einer N x P Matrix resultiert in einer M x P Matrix. Hier wieder ein Schema zur Verdeutlichung:

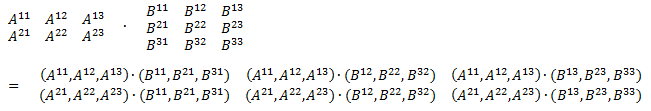
Und nun ein konkretes Beispiel:

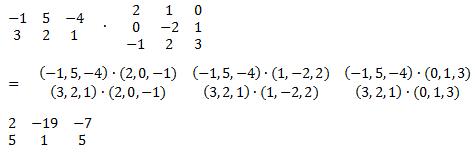
2 x 3 Matrix multipliziert mit einer 3 x 3 Matrix resultiert nach der gegebenen Gleichung in einer 2 x 3 Matrix.

Natürlich kann man auch Vektoren mit Matrizen multiplizieren. Dies geht allerdings nur wenn man die oben angegebene Regel beachtet:

Man kann nur Matrizen multiplizieren wenn die Dimension der Reihen der einen Matrix der Dimension der Spalten der zweiten Matrix entspricht. Das heißt eine M x N Matrix multipliziert mit einer N x P Matrix resultiert in einer M x P Matrix.

Das heißt, man kann einen 1 x 3 Vektor mit einer 3 x 2 Matrix multiplizieren, jedoch mit keiner 2 x 3 Matrix.

Relevante Matrixtypen

5. Lösungen

Die Lösungen wird es in einem später erscheinenden Artikel geben, so dass man sich nicht einfach nur die Lösungen anguckt und die Aufgaben nicht mehr richtig bearbeitet

SideWinder

deren Mathematik statt derer Mathematik.

Freue mich auf diesen Artikel. Viel Erfolg.

MfG SideWinder

Walnut_Burl

Ohh danke!!
Richtig, werde ich eben Editieren.

Michael E.

Ich hab den Artikel nur überflogen, aber auf die Schnelle sind mir drei Sachen aufgefallen:

Vektoren representieren Punkte in Koordinatensystemen

Naja, eher nicht. Hier könntest du IMHO besser von Pfeilen mit Richtungen und Längen reden. Wenn man einen solchen Pfeil vom Ursprung aus zeichnet, kommt man dann auf die Punkte.

Die Länge eines Vektors kann man herausfinden, indem man die Wurzel aus allen seiner Komponenten nimmt, und diese danach addiert.

Nö, so wie es in der Formel steht, ist es richtig.

Es gibt 2 Sonderformen von Vektoren. Erstens kann man den Betrag (Länge) eines Vektors ausrechnen, und zweitens kann man einen Vektor normieren (vereinheitlichen).

Sonderformen würde ich das nicht nennen, eher zwei Dinge, die du mit Vektoren machen kannst. Denn das erste ist nicht mal ein Vektor.

Walnut_Burl

Michael E. schrieb:

Ich hab den Artikel nur überflogen, aber auf die Schnelle sind mir drei Sachen aufgefallen:

Vektoren representieren Punkte in Koordinatensystemen

Naja, eher nicht. Hier könntest du IMHO besser von Pfeilen mit Richtungen und Längen reden. Wenn man einen solchen Pfeil vom Ursprung aus zeichnet, kommt man dann auf die Punkte.

Die Länge eines Vektors kann man herausfinden, indem man die Wurzel aus allen seiner Komponenten nimmt, und diese danach addiert.

Nö, so wie es in der Formel steht, ist es richtig.

Es gibt 2 Sonderformen von Vektoren. Erstens kann man den Betrag (Länge) eines Vektors ausrechnen, und zweitens kann man einen Vektor normieren (vereinheitlichen).

Sonderformen würde ich das nicht nennen, eher zwei Dinge, die du mit Vektoren machen kannst. Denn das erste ist nicht mal ein Vektor.

Zu Punkt 1: Du hast Recht, ich werde dann höchstwahrscheinlich nach den Vektoren noch einen Extrapunkt für Punkte einfügen.
2. Es war etwas falsch formuliert, jetzt sollte es besser sein!
3. Stimmt

Michael E.

Die Länge eines Vektors kann man herausfinden, indem man die Wurzel aus allen seiner Komponenten zum Quadrat nimmt, und diese danach addiert.

Die Länge eines Vektors kann man herausfinden, indem man die quadrierten Komponenten addiert und dann die Wurzel zieht :p

Dummie

Hey,

ich habe direkt eine Frage zu folgendem Teil des Artikels:

Natürlich lässt sich mit Punkten auch rechnen, wobei hier einige Operationen partout keinen Sinn machen würden. Was wäre zum Beispiel die Addition zweier Punkte? Eine Subtraktion zweier Punkte hingegen ist vollkommen legitim, da hierbei ein neuer Vektor, der von Punkt 1 zu Punkt 2 reicht, entsteht.

Ich bin mit der 3D-Programmierung nicht vertraut. Wie ist also die Begründung, dass eine Subtraktion keinen Sinn macht?

Wie gesagt, habe davon keine Ahnung, aber sehe diesen Artikel auch für mich als zukünftige Chance mich mit dem Thema mal genauer auseinaderzusetzen.

Vielleicht würde ja auch dem ein oder anderen Leser meine Frage in den Sinn kommen.

Michael E.

Anscheinend wurde am Artikel weitergearbeitet.

Dummie: Diesen Satz würde ich auch auf keinen Fall stehen lassen, denn die Addition wird natürlich auch gebraucht. Zum Beispiel ist der Mittelpunkt zwischen A und B durch (A + / 2 gegeben.

Walnut_Burl: Was ist für dich der Unterschied zwischen einem Punkt und einem Vektor? Du springst mit den Bedeutungen ein wenig, z. B. wenn du anfängst, zwei Punkte zu subtrahieren. Was unterscheidet einen Punkt dann von einem Vektor?

In DirectX gebraucht man meist den D3DXVECTOR4 Vektortyp, da man so zwischen Punkten und Vektoren unterscheiden kann.

Ich hab noch nie mit DX gearbeitet, behaupte aber einfach mal, dass man diesen Typen genau dann benutzt, wenn man ne vierte Dimension braucht, und nicht, um Vektoren von Punkten künstlich unterscheiden zu können.

Walnut_Burl

Michael E. schrieb:

Anscheinend wurde am Artikel weitergearbeitet.

Genau Ich hatte einige Tage leider keine Zeit mich um diesen zu kümmern, doch jetzt ist die Arbeit wieder in ihrem gewohnten Fluss.

Michael E. schrieb:

Dummie: Diesen Satz würde ich auch auf keinen Fall stehen lassen, denn die Addition wird natürlich auch gebraucht. Zum Beispiel ist der Mittelpunkt zwischen A und B durch (A + / 2 gegeben.

Stimmt. Es gibt eine Punktaddition, wobei ein Durchschnitt ausgerechnet wird. Da dies aber nicht relevant für Graphische Programmierung ist, werde ich darauf nicht eingehen und die These, dass es keine Addition gibt stehen lassen. Eine Addition sähe wie folgt aus:

Michael E. schrieb:

Walnut_Burl: Was ist für dich der Unterschied zwischen einem Punkt und einem Vektor? Du springst mit den Bedeutungen ein wenig, z. B. wenn du anfängst, zwei Punkte zu subtrahieren. Was unterscheidet einen Punkt dann von einem Vektor?

2 Punkte subtrahiert ergeben einen Vektoren der zwischen diesen beiden Punkten liegt. 2 Vektoren hingegen ergeben einen neuen Vektor, der nur die Länge dieser Strecke hat, aber vom Punkt "Origin" ausgeht, und parallel zu diesem Scheinvektor zwischen den beiden "Köpfen" der Vektoren ist, wenn sie subtrahiert werden.

Michael E. schrieb:

In DirectX gebraucht man meist den D3DXVECTOR4 Vektortyp, da man so zwischen Punkten und Vektoren unterscheiden kann.

Ich hab noch nie mit DX gearbeitet, behaupte aber einfach mal, dass man diesen Typen genau dann benutzt, wenn man ne vierte Dimension braucht, und nicht, um Vektoren von Punkten künstlich unterscheiden zu können.

Hab mich verschrieben. Richtiger Ansatz ist im obigen Haupttext...

Wie gesagt, dies ist eine eher fortgeschrittene Technik, von daher weiß ich nicht ob ich sie in diesem ersten Artikel schon mit einbringen soll, oder aber eher noch einen 2., später erscheinenden, rausbringen soll.

Ich hoffe, dass ich nun alle Fragen beantwortet habe!

Geht es nur mir so, oder ist der Titel "Grafische Programmierung" etwas irreführend? Unter grafischer Programmierung verstehe ich die Programmierung mittels einer grafischen Programmiersprache (Simulink, Laview, etc.) und nicht die Programmierung von grafischer Darstellung.

PS: Den Artikel hab ich (sorry) nicht gelesen, ich wurde ja schliesslich vom Titel irregeführt

Walnut_Burl

Tim schrieb:

Geht es nur mir so, oder ist der Titel "Grafische Programmierung" etwas irreführend? Unter grafischer Programmierung verstehe ich die Programmierung mittels einer grafischen Programmiersprache (Simulink, Laview, etc.) und nicht die Programmierung von grafischer Darstellung.

PS: Den Artikel hab ich (sorry) nicht gelesen, ich wurde ja schliesslich vom Titel irregeführt

Ich finde den Namen so eigentlich ganz passend..

Welchen würdest du denn, nachdem du den Artikel gelesen hast ;), vorschlagen?

Michael E.

Walnut_Burl schrieb:

Stimmt. Es gibt eine Punktaddition, wobei ein Durchschnitt ausgerechnet wird. Da dies aber nicht relevant für Graphische Programmierung ist, werde ich darauf nicht eingehen und die These, dass es keine Addition gibt stehen lassen.

In Anbetracht der Tatsache, dass du auf die formal korrekte Definition eines Vektors von Wikipedia verweist, gehe ich mal davon aus, dass du weißt, was ein Vektorraum ist. In einem solchen ist aber die Addition eine grundlegende Operation, sodass du nicht einfach behaupten kannst, dass es sie nicht gibt.

[Edit: Das setzt voraus, dass ich mit deiner Unterscheidung von Punkten und Vektoren nicht einverstanden bin. Einen Punkt würde ich über seinen Abstand zum Ursprung definieren, den ich durch einen Vektor beschreiben kann. Deshalb sind deine Rechenoperationen auf Punkten in meinen Augen Vektoroperationen.]

2 Punkte subtrahiert ergeben einen Vektoren der zwischen diesen beiden Punkten liegt. 2 Vektoren hingegen ergeben einen neuen Vektor, der nur die Länge dieser Strecke hat, aber vom Punkt "Origin" ausgeht, und parallel zu diesem Scheinvektor zwischen den beiden "Köpfen" der Vektoren ist, wenn sie subtrahiert werden.

Wie ist denn die Subtraktion zweier Punkte definiert?

Michael E. schrieb:

Ich hab noch nie mit DX gearbeitet, behaupte aber einfach mal, dass man diesen Typen genau dann benutzt, wenn man ne vierte Dimension braucht, und nicht, um Vektoren von Punkten künstlich unterscheiden zu können.

Hab mich verschrieben. Richtiger Ansatz ist im obigen Haupttext...

Da steht immer noch dasselbe...

Walnut_Burl schrieb:

Welchen würdest du denn, nachdem du den Artikel gelesen hast ;), vorschlagen?

Gute Frage. "Grafik-Programmierung"?

PS: Soll jetzt nicht als vernichtende Kritik gesehen werden, ich habe es nur falsch aufgefasst (was wohl auch an meinem Umfeld liegt). Wenn es nur mir so geht ist alles in Butter

Walnut_Burl

Michael E. schrieb:

Ich hab noch nie mit DX gearbeitet, behaupte aber einfach mal, dass man diesen Typen genau dann benutzt, wenn man ne vierte Dimension braucht, und nicht, um Vektoren von Punkten künstlich unterscheiden zu können.

Hab mich verschrieben. Richtiger Ansatz ist im obigen Haupttext...

Da steht immer noch dasselbe...[/quote]
Wurde gerade noch mal verbessert. Mein System ist abgestürzt, deshalb konnte ich es nicht mehr absenden. Nun sollte aber eigentlich das richtige dort stehen.

Michael E. schrieb:

Darauf wird im neuen Teil noch einmal gesondert drauf eingegangen.

Michael E. schrieb:

In Anbetracht der Tatsache, dass du auf die formal korrekte Definition eines Vektors von Wikipedia verweist, gehe ich mal davon aus, dass du weißt, was ein Vektorraum ist. In einem solchen ist aber die Addition eine grundlegende Operation, sodass du nicht einfach behaupten kannst, dass es sie nicht gibt.

Darauf gehe ich ja schon im Punkt 1.2 ein, wo es um die Mathematik von Vektoren geht. Es gibt nur keine Addition von Punkten, wozu ich auch am Ende von Punkt 2.1 eine Grafik eingestellt habe, die dies noch einmal verdeutlichen soll.

PS: Vektorraum musste ich tatsächlich erst googlen, da wir das in der Schule noch nicht durchgenommen haben (besuche die 9. Klasse und bin 14)

Michael E. schrieb:

[Edit: Das setzt voraus, dass ich mit deiner Unterscheidung von Punkten und Vektoren nicht einverstanden bin. Einen Punkt würde ich über seinen Abstand zum Ursprung definieren, den ich durch einen Vektor beschreiben kann. Deshalb sind deine Rechenoperationen auf Punkten in meinen Augen Vektoroperationen.]

Natürlich kann man Punkte auch so definieren, wobei, laut dieser Definition, Punkte nur Vektoren sind. Dies ist aber falsch. Im Endeffekt sind Punkte die "Köpfe" von Vektoren, doch der restliche Vektor hat nichts mehr mit eben diesen zu tun. Denn: Punkte geben ja keine Kräfte oder ähnliches an, sondern nur Richtungen, in die dann zum Beispiel die virtuelle Kamera blickt.

Tim schrieb:

Gute Frage. "Grafik-Programmierung"?

Einverstanden :D. Vielleicht dann doch Grafik-Programmierung - Nötige Mathematik?

Tim schrieb:

PS: Soll jetzt nicht als vernichtende Kritik gesehen werden

Wurd nicht so aufgenommen.

Michael E.

Walnut_Burl schrieb:

Natürlich kann man Punkte auch so definieren, wobei, laut dieser Definition, Punkte nur Vektoren sind. Dies ist aber falsch. Im Endeffekt sind Punkte die "Köpfe" von Vektoren, doch der restliche Vektor hat nichts mehr mit eben diesen zu tun. Denn: Punkte geben ja keine Kräfte oder ähnliches an, sondern nur Richtungen, in die dann zum Beispiel die virtuelle Kamera blickt.

Wieso eignen sich Punkte denn semantisch besser als Vektoren, um eine Richtung auszudrücken?

Walnut_Burl

Michael E. schrieb:

Walnut_Burl schrieb:

Natürlich kann man Punkte auch so definieren, wobei, laut dieser Definition, Punkte nur Vektoren sind. Dies ist aber falsch. Im Endeffekt sind Punkte die "Köpfe" von Vektoren, doch der restliche Vektor hat nichts mehr mit eben diesen zu tun. Denn: Punkte geben ja keine Kräfte oder ähnliches an, sondern nur Richtungen, in die dann zum Beispiel die virtuelle Kamera blickt.

Wieso eignen sich Punkte denn semantisch besser als Vektoren, um eine Richtung auszudrücken?

Da man um eine Richtung mit Punkte auszudrücken sich um die Länge des Vektors keine Sorgen machen muss, wenn man einen Punkt gebraucht. Dies ist eigentlich nur ein Grund der Effizienz, wobei man hier normalerweise auch normierte Vektoren gebrauchen kann.
Die virtuelle Kamera wird wie eine Pyramide dargestellt in der der Sichtbereich dieser liegt. Befinden sich die Objekte außerhalb dieser Pyramide sind sie entweder nicht mehr im Sichtbereich oder aber zu weit weg. Die "Grundfläche" der Pyramide wird hier mit 4 Punkten angegeben (wobei dies im Endeffekt noch vereinfacht wird).
Punkte werden außerdem dafür gebraucht die eigentliche Position der Kamera darzustellen. Da dies mit einem Vektor unsinnig wäre liegt ja auf der Hand.

rüdiger

Wenn du die Spaltenvektoren als Zeilen schreibst, dann solltest du angeben, dass die transponiert sind (üblicherweise macht man das so $(a, b)^T$ ). Damit man die Vektoren nicht mit Kovektoren verwechselt.

Man verwendet 4D Vektoren und 4x4 Transformationsmatrizen, weil man dann Translation als Matrix darstellen kann. Die Vektoren sind dann aber nicht aus dem |R^4. Es handelt sich nur um eine Einbettung des |R^3. Aber ich kenne die mathematischen Details auch nicht genau.

Michael E. schrieb:

Vektoren representieren Punkte in Koordinatensystemen

Naja, eher nicht. Hier könntest du IMHO besser von Pfeilen mit Richtungen und Längen reden. Wenn man einen solchen Pfeil vom Ursprung aus zeichnet, kommt man dann auf die Punkte.

Naja, aber auch das sind ja nur Spezialformen von Vektoren. Das Zitat aus dem Wikipediaartikel spricht es ja schon an.

Michael E.

Der ganze Artikel ist ein Spezialfall Aber hier gehts ja gerade um den Spezialfall R^2 bzw. R^3 mit allen Standardsachen nur für die Grafikprogrammierung.

Walnut_Burl

rüdiger schrieb:

Man verwendet 4D Vektoren und 4x4 Transformationsmatrizen, weil man dann Translation als Matrix darstellen kann.

Stimmt genau Natürlich benutzt man 4D Vektoren auch um Verwechslungen zwischen Vektoren und Punkten (wie auch schon im Artikel genannt) auszuschließen.

rüdiger schrieb:

Naja, aber auch das sind ja nur Spezialformen von Vektoren. Das Zitat aus dem Wikipediaartikel spricht es ja schon an.

Deshalb hatte ich dieses Zitat auch in den Artikel eingebaut und das selbe ein zweites Mal aufzunehmen fand ich etwas übertrieben, so dass ich selber nur eine (verbesserte) kurze Definierung angab.

rüdiger schrieb:

Wenn du die Spaltenvektoren als Zeilen schreibst, dann solltest du angeben, dass die transponiert sind (üblicherweise macht man das so [latex](a, b)^T). Damit man die Vektoren nicht mit Kovektoren verwechselt.

Um ehrlich zu sein, weiß ich zur Zeit nicht, was du damit ausdrücken willst, da wir dies noch nie durchgenommen haben und ich das Wissen hauptsächlich aus Fachbüchern habe.
Zusätzlich finde ich, dass dies etwas zu sehr in die Materie von Vektoren geht, da es für die Grafik-Programmierung nicht relevant ist.

Michael E. schrieb:

Aber hier gehts ja gerade um den Spezialfall R^2 bzw. R^3 mit allen Standardsachen nur für die Grafikprogrammierung.

Jo das stimmt. Die verwendeten R^4 Vektoren geben ja nur an um welche Art (Punkt, Pfeil) es sich handelt.

Michael E. schrieb:

Der ganze Artikel ist ein Spezialfall

Ist dies negativ mir oder dem Artikel gegenüber?

Michael E.

Walnut_Burl schrieb:

Michael E. schrieb:

Der ganze Artikel ist ein Spezialfall

Ist dies negativ mir oder dem Artikel gegenüber?

Weder noch

In einem solchen Artikel wäre es nicht angebracht und vom Umfang her auch überhaupt nicht machbar, alle verwendeten Begriffe (Vektorräume, Skalarprodukte etc.) in den allgemeinen Versionen einzuführen, sondern du beschränkst dich sinnvollerweise auf die Bedeutungen, die du für die Grafikprogrammierung benötigst. Das Zitat richtet sich eher an rüdiger, weil ich nicht weiß, wieso er gerade bei Vektoren eine (in diesem Zusammenhang recht nutzlose) allgemeine Definition haben will und bei den anderen Sachen nicht.